Il giardino di Archimede  Un museo per la matematica

La diffusione del calcolo

|    l'Analyse des infinimentes petites    |    l'integrazione di equazioni differenziali    |    il problema della brachistocrona    |    la nascita del concetto di funzione    |   

L'Analyse des infinimentes petites.

Un contributo essenziale nello sviluppo e nella diffusione del calcolo leibniziano viene da vari esponenti della famiglia Bernoulli. Nel 1691 Johann soggiorna a Parigi e qui partecipa agli incontri del circolo culturale costituitosi attorno a padre Malebranche. Tra gli altri incontra qui il marchese Guillaume Françoise de l'Hospital (1661-1704) al quale dà lezioni sul nuovo calcolo. Dagli appunti manoscritti relativi ha origine il trattato Analyse des infiniments petits che l'Hospital pubblica anonimo a Parigi nel 1696. Questa prima esposizione sistematica del calcolo differenziale - che sarà completata cinquanta anni dopo con le Lectiones mathematicae de methodo integralium per la parte relativa al calcolo detto da Leibniz ``summatorius'' e ``integralis'' da Jacob in poi - ottiene un grande successo e diviene il testo su cui si formano generazioni di matematici. L' Analyse si apre con alcune definizioni, tra cui quella di differenziale, e con due postulati o ``richieste o supposizioni'':

La parte infinitesima di cui è continuamente aumentata o diminuita una quantità variabile è chiamata differenza di quella quantità [...]
È evidente che la differenza di una quantità costante è nulla o zero, ovvero (ciò che è la stessa cosa) le quantità costanti non hanno differenza[...].
I. Richiesta o supposizione
Si richiede che due quantità la cui differenza è infinitesima possano essere usate indifferentemente l'una per l'altra [...]
II. Richiesta o supposizione
Si richiede che una linea curva possa essere considerata come la collezione di una infinità di linee rette, ciascuna infinitesima, ovvero (ciò che è la stessa cosa) come poligono di un numero infinito di lati, ciascuno infinitesimo, che tramite gli angoli tra essi formati determinano la curvatura della linea [...]

Vengono poi esposte le regole di differenziazione per le ordinarie operazioni e le successive sezioni del volume sono dedicate alla applicazione del calcolo a problemi geometrici come la ricerca delle tangenti, la determinazione di massimi, minimi e flessi di una curva, lo studio della curvatura, delle evolute, delle caustiche, degli inviluppi.
Nella sezione IX si trova la cosiddetta ``regola di L'Hospital''.

* Pagina in mostra IV.1

Guillaume Francois de L'Hospital
Analyse des infiniments petits

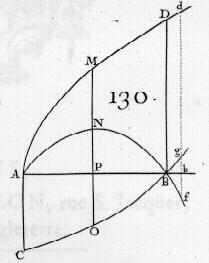
Sia AMD (AP=x, PM=y, AB=a) una linea curva tale che il valore dell'applicata y sia espresso da una frazione il cui numeratore e denominatore diventano ciascuno zero quando x=a, ossia quando il punto P cade sul punto dato B. Si domanda quale debba essere allora il valore dell'applicata BD.

torna a inizio pagina

L'integrazione di equazioni differenziali

Il problema dell'integrazione di equazioni differenziali si presenta fin dall'inizio del calcolo sotto la veste di ``problema inverso delle tangenti''. Si tratta , in breve, di trovare una curva quando sia data una relazione tra la tangente e le coordinate, che nei casi più semplici si scrive analiticamente nella forma $dy/dx=f(x,y)$. Il primo problema di questo tipo fu posto da Florimond De Beaune e risolto da Descartes senza usare il calcolo differenziale: si tratta di trovare una curva la cui sottotangente abbia un valore costante.
Leibniz stesso nella Nova methodus, come immediata applicazione del nuovo calcolo, ne propone una soluzione. In altre formulazioni e varianti si cimentano poi vari matematici.
In termini moderni, ricordando che la sottotangente a una curva $y=y(x)$ è la quantità $y/y'$, tale problema conduce a un'equazione del tipo $y'=ay$, che ha come soluzione $y=Ae^{ax}$.
Una variante del problema che conduce a un'equazione del tipo $y'=a(x-y)$ è cosiderata da Johann Bernoulli che dà anche una costruzione della curva servendosi della curva logaritmica.

* Pagina in mostra IV. 2

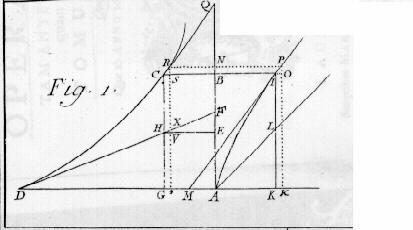
Johann Bernoulli Solutio problematis Cartesio Propositi in Opera [...] Il problema è dunque il seguente: trovare la curva AI tale che la sua ordinata KI sta alla sottotangente KM come un segmento dato N sta al segmento IL dell'ordinata individuato dalla curva AI e dalla retta AL che forma con l'asse AK un angolo pari alla metà di un angolo retto. Soluzione: [...] torna a inizio pagina

Il problema della brachistocrona

Dati due punti in un piano verticale trovare, tra tutti gli archi di curva che li congiungono, la traiettoria che una particella pesante deve percorrere per andare da un punto all'altro in modo che il tempo di percorrenza sia il minore possibile: la questione viene proposta nel 1696 da Johann Bernoulli sugli Acta eruditorum.
Si tratta di uno dei primi problemi di calcolo delle variazioni; in termini moderni si tratta infatti di minimizzare l'integrale che esprime il tempo di discesa in funzione della curva. Sulla differente natura di questo problema rispetto alle questioni di massimo e minimo fino ad allora risolte Jakob Bernoulli osserva:

I geometri hanno fino ad ora utilizzato il metodo dei massimi e minimi per quei problemi in cui fra infinite parti o funzioni di una sola curva data se ne cerca una massima o minima; ma non hanno pensato di applicarla laddove fra le infinite curve non date se ne cerca una a cui competa un qualche massimo o minimo.

Con tecniche diverse e indipendentemente la ``brachistocrona'' (dal greco $\beta\rho \acute{\alpha} \chi \upsilon \sigma \tau o \varsigma$, il piú breve e $\chi\rho\tilde{\omega}\nu o \varsigma$, tempo), detta anche ``oligocrona'' o ``curva celerrimi descensus'', viene determinata da Newton, Leibniz, l'Hospital, Johann Bernoulli e Jakob Bernoulli che l'anno successivo pubblicano, sempre sugli Acta, le loro soluzioni.
Sorprendentemente la nuova curva è la già nota cicloide, per la quale Huygens aveva non molto tempo prima dimostrato anche la proprietà dell'isocronia, vale a dire che le oscillazioni di una particella attorno al punto di equilibrio su una traiettoria cicloidale vengono compiute in tempi uguali indipendentemente dalla loro ampiezza.
La soluzione del proponente Johann riconduce il problema della traiettoria più rapida al problema del cammino di un raggio di luce in un mezzo di indice di rifrazione variabile opportunamente scelto. Servendosi della legge di Snell, per determinare il cammino della luce in un tale mezzo egli considera un certo numero di strati e poi fa tendere il loro numero all'infinito.
La soluzione del fratello Jakob è più geometrica ed è anche piuttosto laboriosa, ma contiene un'idea più generale utilizzabile anche in altri casi. Per determinare i punti della curva Jakob considera incrementi infinitesimi di ascisse, come EC, ed ordinate, come GE, ed inoltre incrementi ottenuti da variazioni a loro volta infinitesime rispetto a questi, come GL rispetto a GE. Con considerazioni geometriche e semplici relazioni tra velocità e spazi percorsi, egli opera su queste quantità infinitesime e quantità infinitesime di quantità infinitesime, ottenendo infine che ascisse e ordinate devono soddisfare la relazione $\frac{EG}{\sqrt{HC}} : \frac{GI}{\sqrt{HE}} = CG : GD$, che caratterizza la cicloide.

* Pagina in mostra IV. 3

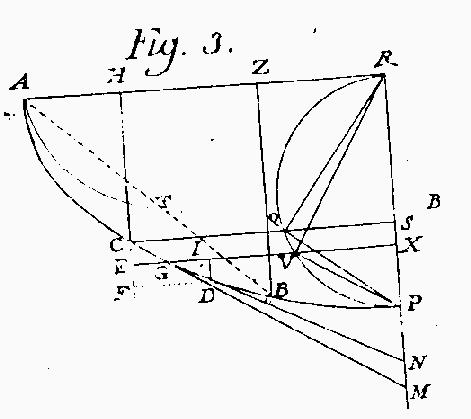
Jacob Bernoulli De curva celerrimi descensus Nello svolgimento proponiamo al celebre Nieuwentijt l'uso dei differenzio-differenziali (che egli ingiustamente rifiuta), laddove siamo costretti ad assumere che il pezzetto GL sia ancora più piccolo di EG e GI già essi stessi infinitamente piccoli; senza di ciò, non vedo come si possa svelare la soluzione del problema. Sono infatti EG, GI elementi dell'ascissa AH, così come CG, GD sono elementi della curva stessa, e HC, HE elementi della stessa sua applicata, e CE, EF sono i loro elementi; così che ricondotto il problema alla geometria pura ci si riduce a trovare la curva i cui elementi siano direttamente proporzionali agli elementi delle ascisse e inversamente proporzionali agli elementi delle ordinate; in verità osservo che gode di questa proprietà l'isocrona di Huygens, da ora in poi anche oligocrona, e comunemente nota ai geometri come cicloide [...]

torna a inizio pagina

La nascita del concetto di funzione

La parola ``funzione'' appare per la prima volta in un manoscritto di Leibniz del 1673 dal titolo Methodus tangentium inversa seu de functionibus e si ritrova in articoli a stampa successivi nonché, ripetutamente, nella corrispondenza con Johann Bernoulli. Il calcolo differenziale di Leibniz, come quello di Newton, ha come oggetto curve: problemi tipici sono quelli di trovare tangenti e quadrature di curve date o di trovare curve a partire da loro proprietà.
Dall'idea di curva come luogo di punti che soddisfano una certa equazione del tipo $P(x,y)=0$, dove P è in generale un polinomio nelle variabili x e y, inizia però a essere focalizzato il fatto che le ``applicate'', cioè le ordinate, dipendono da operazioni effettuate sulle ascisse.
Nel 1718 Johann Bernoulli, in un articolo apparso nelle memorie dell'Académie de Paris dà la seguente definizione:

Chiamo funzione di una grandezza variabile una quantità composta in una maniera qualunque da questa grandezza variabile e da costanti.

È però con Eulero che il concetto di funzione prende il sopravvento su quello meno duttile di relazione. La definizione data all'inzio dell' Introductio in analysin infinitorum è quella di un'espressione analitica costruita a partire dalla variabile $x$ mediante una serie di operazioni.
L'idea di Eulero è che ogni funzione di una variabile possa essere rappresentata come serie di potenze di quella variabile del tipo $A+Bx+Cx2+Dx3+...$. Egli infatti trova tali sviluppi per tutte le usuali funzioni, incluse le trascendenti circolari $\sin x$, $\cos x$, $\arctan x$, e le esponenziali e logaritmiche $e^x$ e $\log(1+x)$. Afferma poi ``Se qualcuno ne dubita il dubbio verrà rimosso dallo sviluppo di ogni funzione'', senza però ovviamente poterne fornire una dimostrazione. Più avanti allora egli dà una generalizzazione della prima definizione, includendo potenze qualsiasi, non solo intere, della variabile:

Affinché questa spiegazione possa essere anche più ampia, oltre alle potenze di z che hanno esponenti positivi, ogni potenza qualunque dovrebbe essere ammessa. Allora non ci sarà più alcun dubbio che ogni funzione di z possa essere trasformata in un'espressione infinita di questo tipo:

$$Az^{\alpha}+Bz^{\beta}+Cz^{\gamma}+Dz^{\delta}+...$$

dove $\alpha$, $\beta$, $\gamma$, $\delta$... denotano numeri qualunque.

L'idea di funzione è ancora lontana da quella moderna: un'importanza preponderante è assunta dal fatto che una funzione sia descrivibile nel suo intervallo di definizione per mezzo di un'espressione analitica singola. Solo più tardi, a seguito di varie discussioni riguardanti in particolare la corda vibrante, Eulero accetterà la possibilità di funzioni cosiddette ``discontinue'', cioè descritte da un'espressione in un intervallo e da una diversa in un altro.

* Pagina in mostra IV. 4

Leonard Euler Introductio in analysin infinitorum Una quantità costante è una quantità determinata che conserva sempre lo stesso valore. Quantità di questo tipo sono i numeri di qualunque genere, dunque ciò che sempre conserva quel valore che ha assunto; e se si devono indicare quantità costanti di questo tipo con dei simboli, si usano le prime lettere dell'alfabeto a, b, c, ecc. Nell'analisi comune dove si considerano soltanto quantità determinate queste prime lettere dell'alfabeto indicano usualmente le quantità note mentre le ultime indicano le quantità incognite; ma nell'analisi sublime questa distinzione non vale più, poiché qui si guarda ad un'altra differenza fra le quantità e cioè alcune si prendono costanti ed altre invece variabili [...] . Una funzione di quantità variabili è un'espressione analitica composta in una maniera qualunque da questa quantità variabile e da numeri o quantità costanti. torna a inizio pagina

Storia del calcolo...

Indice della guida

Pagina successiva

Pagina principale