Il giardino di Archimede  Un museo per la matematica

Metodi di quadratura dall'antichità al Seicento

Teoria delle grandezze e metodo di esaustione

La possibilità di misurare le grandezze, cioè di associare a ognuna di esse un numero che ne esprima il rapporto con una grandezza campione (l'unità di misura) è una delle prime motivazioni per lo sviluppo della matematica, di cui si trovano segni in tutta la produzione preellenica. L'impossibilità della scelta di un'unità di misura universale rispetto alla quale tutte le grandezze omogenee siano esprimibili mediante numeri interi e dunque la necessità di sottomultipli, porta all'introduzione immediata delle frazioni nel sistema numerico, anche se le operazioni con queste non sempre sono pienamente comprese ed esplorate. La matematica greca perfeziona questo sistema numerico, ma la scoperta di grandezze incommensurabili, come il lato di un quadrato e la sua diagonale, fa crollare la costruzione sviluppata dai pitagorici che poneva la scienza del numero alla base di tutto. Se i numeri sono insufficienti a descrivere le cose e in particolare i loro rapporti si relega allora in posizione marginale la teoria dei numeri e si va sviluppando una teoria che permetta di operare direttamente sui rapporti. Questa trova una compiuta sistemazione nella teoria delle proporzioni delle grandezze esposta da Euclide. Da questo punto in poi tutti i risultati sulle grandezze, sostanzialmente fino al Seicento, verranno allora espressi sempre in termini di rapporto o proporzione. Una classe di grandezze (che si diranno omogenee) è ben definita se si sa come eseguire il confronto tra due grandezze della classe (cioè come stabilire quale è maggiore e quale minore) e come eseguirne la somma. Nel caso delle aree delle figure piane o del volume dei solidi la somma è essenzialmente l'unione e il confronto viene eseguito combinando un criterio di inclusione con uno di uguaglianza per equiscomposizione. Per provare che una figura $A$ è uguale a una figura $B$ nel caso in cui non siano equiscomponibili si dovrà provare che non può essere né $A<B$ né $A>B$. Per fare ciò si procede per assurdo; supponendo ad esempio che $A<B$ l'assurdo si raggiunge mediante la costruzione di una figura intermedia tra$A$ e$B$ che dovrebbe risultare contemporaneamente maggiore e minore di $A$. Il metodo di esaustione, attribuito ad Eudosso ed utilizzato nel XII libro degli Elementi di Euclide, rientra nella teoria classica delle grandezze. Il termine esaustione non è usato dai greci ma viene introdotto nel XVI secolo. Si riferisce al procedimento di costruzione della figura intermedia descritto sopra alla cui base sta l'assioma seguente: se da una qualsiasi grandezza si sottrae una parte non inferiore alla sua metà e se dal resto si sottrae ancora non meno della sua metà e se questo processo di sottrazione viene continuato alla fine rimarrà una grandezza inferiore a qualsiasi grandezza dello stesso genere precedentemente assegnata. Questo procedimento che può essere piuttosto lungo e laborioso e richiede di conoscere in precedenza il risultato che si vuole raggiungere permette di provare con rigore che determinate figure stanno tra loro in un certo rapporto o che due figure stanno tra loro come altre due, tanto che nel Rinascimento si diffuse la convinzione dell'esistenza di un metodo segreto da usare preliminarmente. Dalla metà del Cinquecento il problema di ``divinare`` il presunto metodo e di trovare una scorciatoia alle complicazioni che l'esaustione presenta al crescere della generalità dei risultati che accompagna la riscoperta e la restituzione dei classici, costituisce il punto di partenza per l'elaborazione di nuove tecniche.

torna a inizio pagina

|   la quadratura della parabola di Archimede    |    gli indivisibili di Cavalieri    |    l'iperboloide infinito di Torricelli    |   

La quadratura della parabola di Archimede

Nell'introduzione alla Quadratura della parabola Archimede afferma di essere il primo a cimentarsi in questo risultato e dichiara di ottenerne la dimostrazione servendosi di un ``lemma'', variante dell'assioma di esaustione usato in precedenza da altri autori, che oggi è noto come ``principio di Archimede'': date due aree disuguali è possibile, aggiungendo a se stesso l'eccesso di cui la maggiore supera la minore, superare ogni area finita data. Nella proposizione 17 viene data una dimostrazione piuttosto lunga e complessa della quadratura con il procedimento completo secondo il metodo di esaustione. Una seconda e più semplice dimostrazione è contenuta nella proposizione 24, l'ultima dell'opera. Per dimostrare che il segmento parabolico $ADBEC$, che per comodità indichiamo con $P$, ha area uguale a $K$, che è i 4/3 del triangolo inscritto $ABC$, egli dimostra che non può essere né $P$ maggiore di $K$ né $P$ minore di $K$. Nel primo passo questo viene fatto costruendo un poligono, che indichiamo con $S$, per il quale si giunge all'assurdo $K<S$ e $S<K$. Il poligono $S$ è costruito dall'unione successiva del triangolo $ABC$ e di triangoli inscritti nei segmenti parabolici residui. 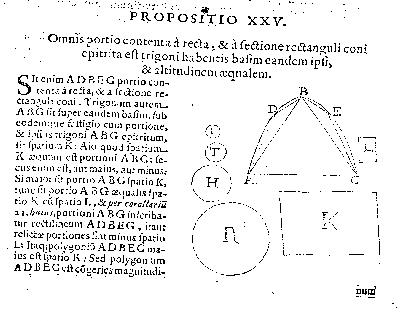Nelle proposizioni precedenti Archimede aveva provato che inscrivendo un triangolo in un segmento parabolico e considerando i due triangoli inscritti nei due segmenti parabolici residui si ha che questi ultimi sommati hanno area pari a un quarto del primo triangolo. Se allora si suppone $P>K$ , ripetendo la costruzione si potrà formare un poligono $S$ tale che $P>S>K$. D'altra parte sarà $S<K$ (si noti che 1+(1/4)+(1/4)2+(1/4)3+...=4/3) e dunque il primo assurdo è raggiunto. In modo analogo si procede nel secondo passo per provare che non può essere $P$ minore di$K$.

* Pagina in mostra I.1

Archimede
Quadratura parabolae, ex traditione Francisci Maurolici

Proposizione 24.
L'area di una qualunque sezione di cono rettangolo è 4/3 del triangolo avente la stessa base e altezza uguale al segmento.

Si noti che la sezione è intesa perpendicolare a una generatrice del cono, dunque la figura ottenuta è una parabola. Nella versione dell'opera di Archimede redatta da Maurolico, che si differenzia in più punti dalla versione classica, la proposizione finale XXIV è divenuta XXV. Il problema della quadratura della parabola costituisce anche il primo degli esempi illustrati nella lettera ad Eratostene scoperta nel 1906 da J. L. Heiberg (Metodo, proposizione 1). Qui Archimede si serve di considerazioni meccaniche sull'equilibrio, utilizzando proprietà dei centri di gravità e delle leve per scoprire meccanicamente i teoremi. Questo metodo euristico per la congettura dei risultati fornisce, a detta dello stesso Archimede, non una vera dimostrazione ma solo un'indicazione sulla conclusione che potrà essere poi dimostrata geometricamente.

torna a inizio pagina

Gli indivisibili di Cavalieri

Rispetto ai metodi classici il metodo degli indivisibili di Cavalieri costituisce un nuovo e potente strumento per la determinazione di aree e volumi. Nelle pagine introduttive della Geometria egli descrive come sia giunto alla sua elaborazione:

Meditando dunque un giorno sulla generazione dei solidi che sono originati da una rivoluzione intorno ad un asse e confrontando il rapporto delle figure piane generatrici con quello dei solidi generati mi meravigliavo moltissimo del fatto che le figure generate si discostassero a tal punto dalla condizione dei propri genitori da mostrare di seguire un rapporto completamente diverso dal loro. Per esempio un cilindro, che sia ottenuto insieme ad un cono della stessa base per rotazione attorno a un medesimo asse, è il triplo di esso, anche se nasce per rivoluzione da un parallelogramma doppio del triangolo che genera il cono. [...]
Avendo dunque più e più volte fermato l'attenzione su tale diversità in moltissime altre figure, mentre prima, raffigurandomi ad esempio un cilindro come l'unione di parallelogrammi indefiniti per numero e il cono con stessa base e stessa altezza come l'unione di triangoli indefiniti per numero passanti tutti per l'asse, ritenevo che ottenuto il mutuo rapporto di dette figure piane dovesse subito venirne fuori anche il rapporto dei solidi da esse generate, risultando invece già chiaramente che il rapporto delle figure piane generatrici non concordava affatto con quello dei solidi generati mi sembrava si dovesse a buon diritto concludere che avrebbe perduto il tempo e la fatica e che avrebbe trebbiato inutile paglia chi si fosse messo a ricercare la misura delle figure con tale metodo.
Ma dopo aver considerato la cosa un po' più profondamente pervenni finalmente a questa opinione e precisamente che per la nostra faccenda dovessero prendersi piani non intersecantisi tra di loro ma paralleli. In questo infatti, investigati moltissimi casi, in tutti trovai perfetta corrispondenza tanto tra il rapporto dei corpi e quello delle loro sezioni piane quanto tra il rapporto dei piani e quello delle loro linee [...].
Avendo dunque considerato il cilindro e il cono suddetti secati non più per l'asse ma parallelamente alla base, trovai che hanno rapporto uguale a quello del cilindro al cono quei piani che chiamo nel libro II ``tutti i piani'' del cilindro a ``tutti i piani'' del cono, con riferimento alla base comune [...]. Stimai perciò metodo ottimo per investigare la misura delle figure quello di indagare i rapporti delle linee al posto di quello dei piani e i rapporti dei piani al posto di quello dei solidi per procurarmi subito la misura delle figure stesse. La cosa, ritengo, andò come era nei miei voti, come risulterà chiaro a chi leggerà tutto.

Nel primo e secondo libro espone dunque le ``proposizioni lemmatiche'', cioè i lemmi sui quali si basa il suo metodo, introduce il concetto di ``tutte le linee'' di una figura piana e di ``tutti i piani'' di una figura solida e stabilisce che ``tutte le linee'' di figure piane (e analogamente ``tutti i piani di figure solide'') sono grandezze che hanno tra loro rapporto, risultato fondamentale per poter operare con esse. Nei libri successivi dimostra poi risultati relativi a figure piane e solide originate dalle sezioni coniche e dalle spirali. Il metodo degli indivisibili fu oggetto di numerose critiche. Cavalieri tentò di prevenirle in parte nella stessa Geometria: nel libro VII egli espone quello che chiamerà ``secondo metodo'' in cui chiarisce i fondamenti degli indivisibili e che si fonda su teorema I, ancor oggi noto come ``principio di Cavalieri''

* Pagina in mostra I.2

Bonaventura Cavalieri Geometria indivisibilibus quadam ratione promota Teorema I. Proposizione I. Figure piane qualsiasi, poste tra le stesse parallele, in cui, condotte linee rette qualunque equidistanti alle parallele in questione, le porzioni così intercettate di una qualsiasi di queste rette siano uguali, sono parimenti uguali tra loro. E figure solide qualsiasi, poste tra gli stessi piani paralleli, in cui, condotti piani qualunque equidistanti a quei piani paralleli, le figure piane di uno qualsiasi dei piani condotti così determinate nei solidi siano uguali, saranno parimenti uguali tra loro. Si chiamino allora tali figure ugualmente analoghe, sia le piane che le solide confrontate tra loro, e rispetto alle linee di riferimento, o i piani paralleli, tra i quali si suppongono poste, se è necessario indicarlo.

torna a inizio pagina

L'iperboloide infinito di Torricelli

Uno dei risultati ottenuti da Torricelli con l'applicazione del metodo degli indivisibili che più riscosse l'ammirazione dei contemporanei fu il calcolo del volume del solido iperbolico. Tale problema ``a degli aspiranti Geometri, sembrerebbe non solo difficile, ma addirittura impossibile'', egli scrive nell'introduzione e continua:

Infatti nelle trattazioni scolastiche di geometria si trovano misure di figure limitate da ogni parte e [...] nessuno che io sappia ha estensione infinita. E se si propone di considerare un solido oppure una figura piana infinitamente estesa ciascuno pensa subito che una figura di questo genere debba essere di grandezza infinita. Eppure esiste un solido di grandezza infinita ma dotato di una sottigliezza tale che per quanto prolungato all'infinito non supera la mole di un piccolo cilindro. Esso è il solido generato dall'iperbola [...]

che Torricelli chiama anche ``solido acuto iperbolico''. Anche Cavalieri rimase stupito da tale risultato e in una lettera a Torricelli scrive:

Non so come abbi pescato nell'infinita profondità di quel solido così facilmente la sua dimensione poiché veramente a me pare infinitamente lungo.

La dimostrazione data da Torricelli è duplice: accanto a quella con gli indivisibili compare anche una dimostrazione per soddisfare anche ``il lettore poco amico degli Indivisibili'' [...] ``con il metodo solito di dimostrazione degli antichi geometri, il quale è bensì più lungo ma non per questo, secondo me, più sicuro''. Nell'introduzione si ha un elogio della Geometria degli indivisibili ``la quale è un vero modo scientifico di dimostrare, diretto e per così dire naturale'' che, sull'entusiasmo degli orizzonti aperti dalla nuova scoperta, porta Torricelli ad affermare:

Mi muove a compassione la vecchia geometria , la quale, non conoscendo oppure non ammettendo gli indivisibili, nello studio dei corpi solidi scoprì così poche verità che una penosa povertà di idee è perdurata fino all'età nostra. Infatti i teoremi degli antichi che compongono la dottrina dei solidi rappresentano soltanto una parte delle speculazioni che, nella nostra epoca il mirabile Cavalieri, per non parlare di altri, fece attorno a numerose classi di solidi, differenti di specie e abbondanti in gran numero``.

* Pagina in mostra I. 3

Evangelista Torricelli
Sulla misura della parabola e del solido iperbolico

Teorema
Il solido acuto iperbolico infinitamente lungo, tagliato con un piano perpendicolare all'asse, insieme con il cilindro della sua base, è uguale ad un cilindro retto la cui base sia il lato verso, ovvero l'asse dell'iperbola, e la cui altezza sia uguale al semidiametro della base del solido acuto.

Torricelli afferma dunque che il solido FENBLD di rotazione attorno all'asse BA è uguale al cilindro avente per altezza AC e per base il cerchio di diametro AH, dove AH è il lato verso dell'iperbole. Il metodo usato da Torricelli fa uso degli indivisibili curvi, che illustra in precedenza con alcuni esempi ``non avendo Cavalieri nella sua Geometria fatto alcun cenno a tali cose''. Gli indivisibili curvi usati per il paraboloide sono le superfici cilindriche descritte dalla rotazione di un qualsiasi segmento congiungente un punto dell'iperbole con l'asse AC, come nella figura IL. Per le proprietà dell'iperbole, al variare del punto I le superfici cilindriche ONLI saranno uguali ai cerchi di diametro IM ottenuti dalle sezioni piane del cilindro ACGH. Dunque, usando la teoria degli indivisibili, tutte le superfici cilindriche prese insieme saranno uguali a tutti i cerchi presi insieme, cioè il solido ``acuto iperbolico'' sarà uguale al cilindro.

torna a inizio pagina

Storia del calcolo...

Indice della guida

Pagina successiva

Pagina principale