Un museo per la matematica
della trigonometria
| Il giardino di Archimede
Un museo per la matematica |
Breve storia
della trigonometria |
La trigonometria greca.L'invenzione della trigonometria si può associare con un certa sicurezza agli studi astronomici della scuola geometrica di Alessandria. La città egiziana di Alessandria, che porta il nome di ALESSANDRO MAGNO che la fondò nel III secolo a. C., fu la capitale del regno ellenistico dei TOLOMEI fino alla conquista romana. La sua posizione centrale nel mondo mediterraneo dell'antichità, una politica culturale illuminata da parte dei governanti, che la dotarono di una biblioteca famosa per più di un millennio, una delle sette meraviglie del mondo, fecero di Alessandria il centro della matematica greca fin quasi alla conquista araba, e il ponte attraverso il quale la geometria classica è pervenuta, mediante la tradizione araba, fino all'età moderna. Uno dei tratti della matematica alessandrina, accanto agli studi di matematica pura che proseguirono vigorosi per vari secoli, fu un'attenzione costante per le applicazioni scientifiche e tecniche, e di conseguenza per una matematica quantitativa, attraverso la quale i risultati teorici della geometria classica potevano trovare il loro corrispettivo nelle scienze della natura. Vengono così sviluppate, accanto alle matematiche tradizionali, una serie di nuove discipline, che oggi chiameremmo col nome di matematica applicata, che spaziavano dall'ottica alla pneumatica, dalla meccanica alla geodesia. Questo nuovo punto di vista trova un terreno particolarmente favorevole in astronomia, dove a un'indagine prevalentemente cosmologica, mirante cioè a indagare la struttura dell'universo e le cause dei moti degli astri, il cui massimo esempio sono le opere aristoteliche, in particolare la Fisica e il trattato Del cielo, si sostituisce un'astronomia quantitativa, capace di prevedere i fenomeni celesti (posizioni dei pianeti, eclissi, congiunzioni) e quindi di essere di aiuto in una serie di attività umane, come la determinazione dell'ora, la misura dell'anno, la geografia, la navigazione, e non ultimo la compilazione degli oroscopi. L'astronomia quantitativa ha bisogno di una geometria altrettanto quantitativa, in particolare di una geometria della sfera, dato che sulla sfera celeste si svolgono i moti di cui si vuole costruire una teoria. Di qui la spiegazione del fatto che gli inventori della trigonometria sono gli stessi astronomi che l'avrebbero applicata allo studio del cielo, e di quello un po' paradossale che la trigonometria sferica (cioè lo studio dei triangoli sferici, tracciati sulla superficie della sfera e i cui lati sono archi di cerchio) preceda storicamente la trigonometria piana, contro la scala naturale delle difficoltà. Il fondatore della trigonometria è probabilmente IPPARCO DA RODI (II sec. a. C.), che visse per lo più ad Alessandria, anche se prima di lui avevano trattato brevemente di geometria sferica EUDOSSO di Cnido (c. 408-365 a. C.) ed EUCLIDE di Alessandria (III sec. a. C.), meglio noto come l'autore degli Elementi. Contributi fondamentali alla trigonometria sferica sono dovuti a TEODOSIO di Tripoli (I sec. a. C.) e MENELAO di Alessandria (I-II sec. d. C.), ambedue autori di volumi noti col titolo di Sphaerica. Ma la maggior parte di notizie sui metodi trigonometrici alessandrini ci vengono dal massimo astronomo dell'antichità: TOLOMEO CLAUDIO (II sec. d. C.), che con la sua opera dal titolo Composizione matematica, che poi venne mutato in Grande composizione (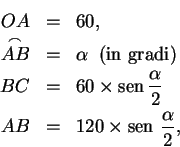
e quindi, se indichiamo con ossia Nel primo libro dell'Almagesto di TOLOMEO troviamo tra le altre cose una tavola delle corde, che procede di mezzo grado in mezzo grado da In questo modo, si riesce a risolvere ogni triangolo rettangolo. I triangoli generali venivano poi ricondotti a triangoli rettangoli. Più complessa è la costruzione della tavola delle corde. Queste infatti sono note solo per alcuni angoli (quello di 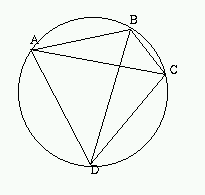
Tolomeo si serve di questo teorema nel caso in cui 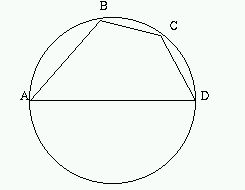
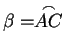 , si ha , si ha
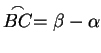 , ,
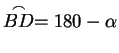 e e
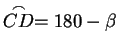 . Dal teorema di
Tolomeo segue allora . Dal teorema di
Tolomeo segue allora
D'altra parte, i triangoli 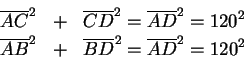
e quindi 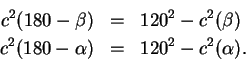
Di conseguenza, nella (1.1) tutti i termini sono noti, e si può ricavare la corda di La (1.2) è equivalente al teorema di sottrazione dei seni; infatti, se ricordiamo che 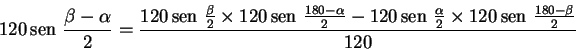
da cui, semplificando ovvero, dato che Con un metodo simile si trova la formula di bisezione. Se infatti prendiamo 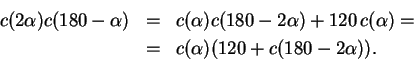
Elevando al quadrato ambo i membri, e tenendo conto che e risolvendo ![\begin{displaymath}c^{2}(\alpha) = \frac{120^{2} c^{2}(2\alpha)}{[120+c(180-
2\alpha)]^{2}+c^{2}(2\alpha)}. \end{displaymath}](img54.gif)
Quest'ultima è già una formula di bisezione, in quanto dalla corda dell'arco 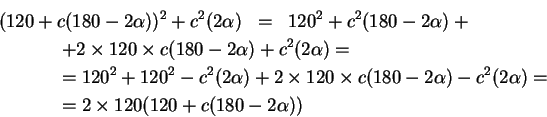
e quindi in conclusione Tramite questa equazione, TOLOMEO può calcolare le corde corrispondenti ad angoli sempre più piccoli. In particolare, dalla conoscenza degli angoli di 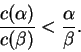
Applicando questa diseguaglianza agli angoli 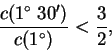
mentre se si prende 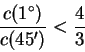
e quindi una formula che consente di trovare la corda di |