II Esercitazione di Matematica I del 28 gennaio 2005

(CHIMICA e CHIMICA APPLICATA, a.a. 2004-2005)

Esercizio 1) – Trovare le soluzioni del seguente sistema lineare al variare del parametro l

lx – y + 2z = 0

y + z = 0

x – y = 0.

Esercizio 2) – Un punto si muove su una retta con accelerazione a(t) = (t + 1).

Determinare la velocità all’istante t = 3 supponendo che il punto parta da fermo.

Determinare lo spazio percorso nello stesso intervallo di tempo.

Esercizio 3) – Disegnare il grafico approssimato (senza risolvere l’integrale) della funzione

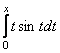
Verificare il risultato dopo aver risolto l’integrale.

Esercizio 4) – Calcolare l’area della regione piana limitata compresa tra il grafico della funzione F(x) = e la retta passante per l’origine con coefficiente angolare 1/2 .

Calcolare il volume del solido che si ottiene facendo ruotare tale regione intorno all’asse x.