Il teorema del limite centrale all'opera

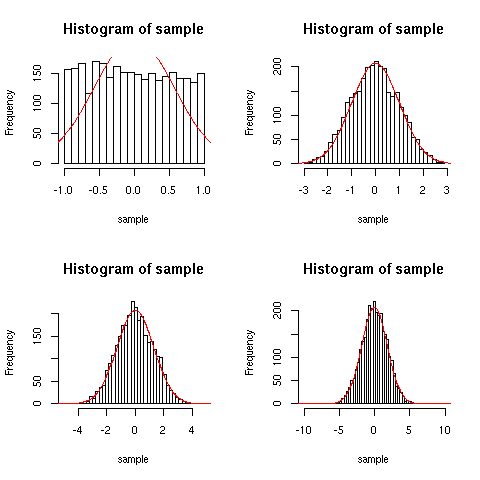
Per dimostrare l'importanza pratica del teorema del limite centrale, confrontiamo la distribuzione della somma di $n$ variabili distribuite uniformemente nell'intervallo $[-1,1]$. Come visto in precedenza, la distribuzione per $n=2$ è una funzione triangolare. Più in generale, la funzione densità è descritta da polinomi di grado $n-1$ e solo nel limite $n\to\infty$ diventa una gaussiana. Tuttavia, per un valore finito del numero di osservazioni $N$, la distribuzione può essere descritta da una gaussiana con ottima approssimazione già per valori di $n$ molto bassi:

centrallimit <-function(n,N=1000) {
 sample = runif(N,-1,1)
 if (n >1) {
  for (i in 1:(n-1)) {
   sample = sample + runif(N,-1,1)
  }
 }
 delta=sqrt(n)/10
# confrontiamo la distribuzione ottenuta con la gaussiana
# che ci aspettiamo dal teorema del limite centrale
 hist(sample,breaks=seq(-1*n,1*n,delta))
 curve(dnorm(x,sd=2*sqrt(n/12))*N*delta,add=T,col="red")
}

par(mfrow=c(2,2))
centrallimit(n=1,N=3000)
centrallimit(n=3,N=3000)
centrallimit(n=5,N=3000)
centrallimit(n=10,N=3000)