LE SPIRALI AUREE

Evangelista Torricelli (1608-1647) ha scritto il “De spiralibus infinitis” in cui presenta le proprie ricerche,ampie e complete, su particolari spirali che prenderanno proprio il suo nome.

Sono “spirali” quelle curve piane che si ripetono indefinitamente compiendo giri intorno ad un punto fisso O (polo).Dice Torricelli: “ il punto mobile……nelle nostre spirali…..percorre in tempi uguali spazi in progressione geometrica,quindi piacque chiamare geometriche queste spirali”.

Osserviamo che per il modo come le spirali vengono definite,gli archi opposti ad angoli a uguali (percorsi dunque in intervalli costanti di tempo),hanno raggi vettori (segmenti che unicono gli estremi degli archi con il polo) in progressione geometrica.

Perciò in un riferimento polare in cui O è il polo e la retta che contiene AO (AO=1 [u] ) è l’asse polare,al tempo t le coordinate di un generico punto che descrive una spirale sono (in relazione ad un determinato valore q della ragione della progressione geometrica) :   r = q^t     ; q = t a

Al variare di t con continuità (e dunque eliminando il parametro  t ) si ottiene l’equazione polare della spirale:    r  =  q^q/a   .

Nella seconda metà del XVII sec.,tra gli altri interessi dei matematici vi è quello verso il numero d’oro : dal binomio “spirale di Torricelli-numero d’oro” hanno tratto origine la spirale aurea dei triangoli rotanti e la spirale aurea dei quadrati rotanti.

LA SPIRALE AUREA DEI TRIANGOLI ROTANTI

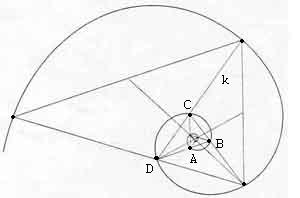La spirale passa per i vertici di un insieme di triangoli aurei costruiti l’uno dall’altro in base ad una determinata legge,fissato il senso del movimento e posto il polo nell’intersezione di mediane omologhe.Spostiamoci in senso antiorario  e consideriamo il triangolo aureo ABC,di cui raddoppiamo l’angolo C =p/5 tramite la semiretta k; sia D il punto comune alla retta per A,B ed a k;il triangolo BCD,anch’esso aureo,è ottenuto dal precedente mediante una rotazione di 3p/5 intorno ad O,punto comune alle mediane omologhe AM e BN. Si prosegue con lo stesso criterio e si riconosce che le mediane dei successivi triangoli aurei passano per O, da cui i vertici dei triangoli sono tutti visti sotto il medesimo angolo 3p/5; la spirale in fig 1, traendo inizio da A, passa successivamente per B,C,D,…è dunque equiangolare: essa non ha inizio né fine, ma si avvolge indefinitamente anche all’interno del triangolo ABC. Con metodi elementari si trova BO/OA=CO/BO=……=t; i raggi vettori sono quindi in progressione geometrica di ragione t. L’equazione della spirale è : r=t^5q/3p

LA SPIRALE AUREA DEI QUADRATI ROTANTI

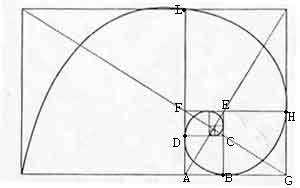Questa spirale trae origine da rettangoli aurei.Nel rettangolo  aureo ABEF  di lati  1 e t, si evidenzia il quadrato ABCD di lato 1 e ne rimane il rettangolo aureo DCEF ;tramite il quadrato BGHE,di lato t, si ha un nuovo rettangolo aureo AGHF.Si prosegue  in senso antiorario con il quadrato di lato FH=1+t , e così via.Dunque dal primo quadrato si passa al secondo, al terzo,…,con una rotazione di p/2 attorno al punto O,comune alle diagonali omologhe in rettangoli simili.In figura la spirale aurea  dei quadrati rotanti parte da D e “tocca” successivamente B,H,L,….   : essa non ha inizio né fine, ma si avvolge indefinitamente anche all’interno del rettangolo DCEF.

Si riconosce che i raggi vettori sono in progressione geometrica di ragione t,e le corde DB,BH,…sono tutte viste da O secondo un angolo di p/2. Ne segue l’equazione r=t^2q/p  .