Il Calcolo Numerico: un paio di applicazioni

1. Le formule di quadratura: come si calcolano gli integrali.

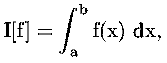
supponendo di conoscere la funzione f(x) e che questa sia continua. Supponiamo poi di essere in grado di calcolare i valori di f(x) con l'accuratezza desiderata. Il primo metodo che viene in mente è suddividere l'intervallo di integrazione in un certo numero di intervallini,

ed approssimare il valore dell'area del sottografico della funzione con quella dell'unione dei rettangoli aventi per base l'intervallo [x_i-1, x_i] e altezza f(x_i).

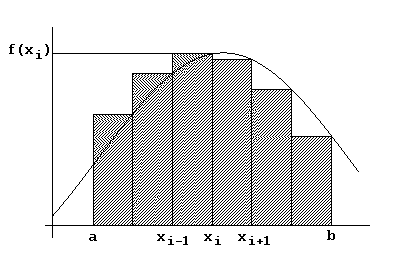
In pratica, abbiamo approssimato il valore dell'integrale con

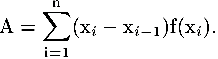
Avremmo potuto scegliere anche f(x_i-1) come altezza dei rettangoli. La formula ottenuta sarebbe stata simile ma avrebbe fornito un valore numerico differente dal precedente. Quale dei due valori è migliore? E soprattutto, cosa significa in questo caso la parola "migliore"?

Iniziamo l'analisi cercando una stima dell'errore che si commette sostituendo alla funzione f(x) una funzione costante a tratti (è un altro modo di descrivere quello che abbiamo fatto calcolando l'area dei rettangoli al posto dell'integrale di f(x)).
Qualunque risultato numerico, non solo il risultato del calcolo di un integrale ma anche, per esempio, la soluzione di un sistema lineare, o la soluzione approssimata di un equazione numerica o differenziale, non è utile se presentato da solo, senza altre informazioni. Ha significato solo se accompagnato da una stima dell'errore commesso o comunque da qualcosa che permetta di valutarne l'attendibilità.
Nel caso in cui si cerchino, le soluzioni di un equazione, se si usa ad esempio il metodo di bisezione, il metodo stesso fornisce una stima dell'errore. Se invece si usa il metodo delle corde, non siamo in grado di fornire una stima dell'errore ma, se x₀ è il valore ottenuto per la soluzione, |f(x₀)| può essere utile a valutare il risultato ottenuto.

Cerchiamo una stima dell'errore per la nostra formula di quadratura. Sia A il valore fornito dalla formula. Vogliamo trovare due quantità A₁ e A₂ tali che

In questo caso potremo affermare che A è un valore che approssima I[f] e che l'errore commesso non supera A₂-A₁. Il numero di cifre "esatte" di A è dato dal numero di ordini di grandezza di differenza tra A₂-A₁ ed A stesso (si osservi che se il valore esatto è 2.000 e come valore approssimato otteniamo 1.999, si dice che il valore ottenuto ha 3 cifre esatte anche se in effetti sono tutte differenti.

Le cifre esatte sono soltanto un modo per quantificare l'errore relativo ).
Nel nostro caso, se come altezza dei rettangolini scegliamo il min{f(x_i-1), f(x_i)}, otteniamo una approssimazione per difetto del valore di I[f]:

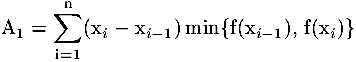
Analogamente, se invece del minimo scegliamo il massimo tra i 2 valori, otteniamo una approssimazione per eccesso:

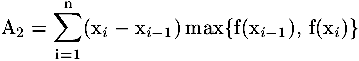
Possiamo quindi scrivere una prima stima dell'errore:

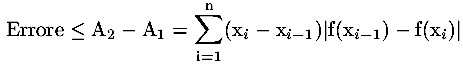
Se supponiamo che la funzione sia derivabile con derivata continua, allora, per il teorema di Lagrange si ha:

f(x_i)-f(x_i-1)= f'(t)(x_i-x_i-1)

dove x_i-1< t < x_i. Quindi, se

M=max{|f'(t)| : a< t < b},si ha: |f(x_i)-f(x_i-1)|< M |x_i-x_i-1|.

Utilizziamo la maggiorazione appena ottenuta nella formula scritta sopra per l'errore:

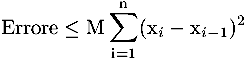
Una scelta piuttosto comune è prendere gli x_i equidistanti; in questo caso,

x_i - x_i-1 = (b-a)/n.

La stima che ricava è piuttosto semplice da interpretare:

Errore < M (b-a)²/n

Si vede chiaramente in che modo l'errore dipenda dal numero delle suddivisioni. Inoltre si può osservare che le funzioni più "difficili" da integrare sono quelle fortemente oscillanti (cioè con M grande), cosa che era da aspettarsi, data la maggiore difficoltà di approssimarle fedelmente con i rettangoli.

L'applicazione che segue utilizza il metodo dei rettangoli, modificato in vari modi, ma utilizza anche alcuni metodi più raffinati, come ad esempio il metodo dei trapezi. Anche per i trapezi è possibile, anche se è un po' più complicato, ottenere stime dell'errore:

Errore_trapezi = M₂ (b-a)³/n³ dove M₂=max{|f"(t)| : a< t < b}.

Con f" si indica la derivata seconda di f.
Il metodo dei trapezi è più accurato del precedente, come si può osservare dal fatto che l'errore dipende dal cubo del numero di suddivisioni. Questo permette di raggiungere ottime approssimazioni con un numero relativamente piccolo di suddivisioni.
I metodi proposti fanno tutti parte di una stessa categoria, quella delle formule di Newton-Côtes. Viene calcolato esattamente, cioè senza errori dovuti al metodo, l'integrale del polinomio interpolante la funzione negli x_i scelti (interpolante significa che passa per i punti (x_i, f(x_i)) ). A seconda del grado scelto per il polinomio si ottengono i vari metodi; per esempio se il grado è 0 si ha il metodo dei rettangoli, se è 1 si ha il metodo dei trapezi.

Questa applet calcola l'area sotto il grafico di una funzione data. La funzione di default è f(t) = 1/t. È possibile cambiare la funzione clickando sul pulsante "Function" e gli estremi di integrazione sia spostandoli con il mouse che scrivendo il valore nelle finestre. Si può anche scegliere il metodo di integrazione. È possibile soprattutto confrontare, anche visivamente, la differenza di accuratezza tra il metodo dei rettangoli e quello dei trapezi a parità del numero n di suddivisioni.

Ringraziamo il prof. Paul Caprioli caprioli@middlebury.edu, visiting professor al Middlebury College, che ci ha gentilmente concesso la possibilità di utilizzare l'applet, di cui è unico autore, in questo testo.

2. Soluzione di equazioni non lineari

dove f(x) è una opportuna funzione. Prima di esaminare degli algoritmi per determinare le soluzioni di una equazione è necessario chiarire che cosa significa "risolvere" l'equazione. Infatti solo raramente è possibile determinarne le soluzioni esatte e questo può accadere per vari motivi.
Facciamo un paio di esempi:

• È noto che anche per funzioni piuttosto semplici, per esempio polinomi di grado > 4 non è possibile scrivere formule risolutive in forma chiusa (cioè in cui compaiono solo un numero finito di operazioni elementari). Questo obbliga ad usare metodi iterativi che portano necessariamente a valori approssimati per le soluzioni.

• I calcoli sono svolti in precisione finita: i numeri reali sono rappresentati nei calcolatori secondo un sistema detto virgola mobile normalizzata. Non descriveremo nei particolari questo metodo di rappresentazione; ci limiteremo ad osservare che è rappresentabile in macchina esattamente solo un sottoinsieme finito di reali. Tutti gli altri sono affetti fin dall'inizio da un errore di rappresentazione che varia a seconda della precisione di macchina (cioè a seconda di quante cifre binarie sono usate per rappresentare ciascun reale). Un valore tipico per l'errore relativo è circa 10^-7. Nonostante questo valore sia piuttosto piccolo, ci sono casi in cui può portare a seri problemi di calcolo.
  Consideriamo ad esempio l'equazione x²- 2x + 1 = 0: ha come soluzione x = 1. Se però modifichiamo il termine noto aumentandolo di una quantità anche piccolissima, l'equazione non ha più soluzioni reali, ovvero a una piccola modifica sull'equazione può corrispondere una situazione completamente diversa delle soluzioni. Questo fenomeno si chiama instabilità delle soluzioni.