Andrea Colesanti

I Frattali

Un semplice esempio
Qualche immagine
Bibliografia

1. Un semplice esempio.

I frattali: ecco un argomento del quale si sente parlare spesso anche al di fuori degli ambienti più tipicamente "matematici". Ma che cosa sono i frattali? La nozione di insieme frattale è strettamente legata al concetto di "dimensione" di un insieme. Consideriamo alcuni oggetti geometrici familiari: una retta, una circonferenza, un piano, la superficie di una sfera, un cubo ecc. A ciascuno di questi insiemi siamo in grado di associare la sua "dimensione": la retta e la circonferenza hanno dimensione 1, mentre il piano e la superficie della sfera hanno dimensione due; il cubo, in quanto oggetto "pieno", ha dimensione tre e, per contro, il punto ha dimensione zero. In tutti questi casi la dimensione è un numero intero.
Esistono insiemi di dimensione non intera? La risposta è si, ovvero si possono definire, non disegnare, degli insiemi che hanno una struttura geometrica così complicata e lontana dalla semplicità degli insiemi considerati prima, da non permettere di attribuire loro una dimensione "intera".
Nasce così il problema di estendere la nozione di dimensione di un insieme, in modo da prevedere, ad esempio, l'esistenza di insiemi di dimensione 3/2. Questo problema è stato affrontato e risolto da grandi matematici, ed esiste ora una definizione di dimensione, per la verità non semplicissima, che contempla l'esistenza di insiemi che abbiano per dimensione un qualunque numero reale positivo. I frattali sono appunto esempi di insiemi di dimensione non intera.

Anche se i frattali possono sembrare oggetti astratti e lontani dalla vita quotidiana non è così: potrà sembrare sorprendente ma ogni giorno ciascuno di noi si imbatte in qualcosa di molto simile ad un frattale come ad esempio alcuni tipi di foglie o di piante (i pini montani per esempio: dal tronco partono dei rami da cui partono altri rami ecc. ecc., per finire con gli aghi di pino), il profilo di un paesaggio roccioso (se non ci sono punti di riferimento, quali ad esempio una persona, è difficile stabilire quali siano le dimensioni reali di una roccia in una fotografia: montagna o sassolino?) oppure il "frattale" per eccellenza: il fiocco di neve che se osservato al microscopio rivela la sua struttura quasi frattale.
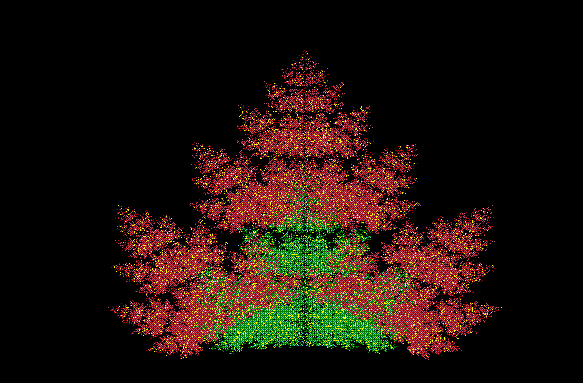
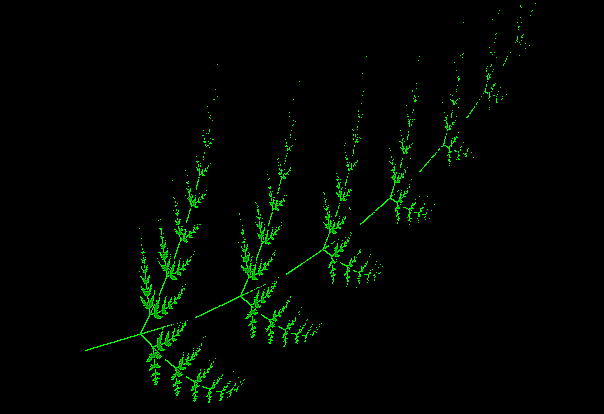
Nelle figure seguenti sono raffigurati un paio di insiemi frattali: è facile rendersi conto della somiglianza della loro forma con quella delle foglie.

Vediamo adesso come si costruisce un semplice insieme frattale: l'insieme di Koch. Si parte da un triangolo equilatero di lato uno e su ciascuno dei suoi tre lati si costruisce un altro triangolo equilatero, di lato 1/3, centrato sul lato, come indicato nella figura 1.

Figura 1.

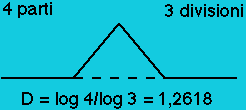
Su ciascuno dei due lati "liberi" dei tre nuovi triangoli, si costruisce un nuovo triangolo equilatero di lato 1/9 e si ottiene così l'insieme più a sinistra in figura 2:

Figura 2.

Il procedimento può essere ripetuto un numero arbitrario di volte: ad ogni passo si costruiscono su ciascuno dei lati liberi dei triangoli aggiunti al passo precedente, dei nuovi triangolini di lato un terzo dei precedenti. Dopo "infinite" iterazioni di questo procedimento, si arriva ad un insieme che chiamiamo K, noto appunto come l'insieme di Koch. Il numero D che compare nella figura 1 è la dimensione dell'insieme di Koch.

Se vedi questa scritta significa che il tuo browser non supporta il linguaggio JAVA e quindi non è in grado di eseguire le applet.

Clicka nel riquadro per vedere le fasi di costruzione della curva.

K non può essere "disegnato" ma solo, diciamo, intuito o immaginato; inoltre si possono disegnare figure che approssimano K con precisione arbitraria. L'insieme K ha dimensione non intera ed è pertanto un insieme frattale. Questo insieme presenta un'altra delle caratteristiche di molti degli insiemi frattali. Immaginate di avere su un foglio davanti a voi una figura dell'insieme K (ribadiamo che questo non è materialmente possibile ma può essere immaginato) e di poter esaminare K con un microscopio il cui grado di definizione possa essere reso alto a piacere. Dando una prima occhiata a K, con un certo grado di definizione, si riesce a distinguere solo un numero finito dei triangolini che formano K. Puntando il microscopio ripresenta la stessa struttura che era stata osservata prima.
L'insieme K ripropone in ogni sua parte copie infinitamente piccole di una stessa struttura di partenza; questa caratteristica si chiama "autosimilarità" dell'insieme.

2. Qualche immagine.

Vi proponiamo alcune immagini, elaborate da computer, di insiemi frattali "famosi" come l'insieme di Mandelbrot e l'insieme di Julia.
La costruzione di questi insiemi può essere descritta "matematicamente" come nel caso dell'insieme di Koch anche se in questo caso il procedimento è più "analitico" che geometrico. Tale costruzione richiede comunque la conoscenza di strumenti matematici di grado abbastanza elevato ma si basa sempre su un procedimento iterato infinite volte.

L'insieme di Mandelbrot
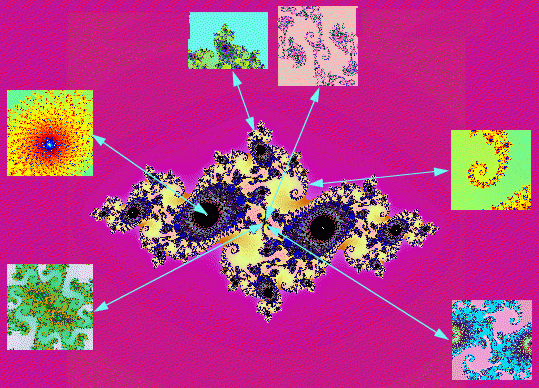
Nella immagine più grande si può vedere l'insieme di Mandelbrot intero. Le altre immagini sono degli ingrandimenti di alcune sue parti.
L'insieme è la parte colorata in bianco nel centro dell'immagine. La parte "interessante", da cui si ottengono le strane immagini riportate sotto, non è l'insieme ma il suo complementare, o meglio il complementare in prossimità del suo bordo. La stessa cosa vale pure per l'insieme di Julia (vedi più avanti).

Il bordo di questi insiemi nonostante sia incredibilmente frastagliato è formato da una unica linea continua (sarebbe cioè possibile teoricamente disegnare il contorno dell'insieme di Mandelbrot senza staccare mai la penna dal foglio). Domini con questa proprietà si chiamano semplicemente connessi. Intuitivamente si potrebbe dire che un dominio è semplicemente connesso se "è fatto da un pezzo solo e non ha buchi al suo interno".

Gli insiemi di Julia
Il modo di costruirlo è molto simile a quello usato per l'insieme di Mandelbrot. Sarebbe più corretto parlare di insiemi di Julia, al plurale. Con insiemi di Julia si indica infatti una famiglia di insiemi dipendente da un parametro. Cambiando i valori del parametro si ottengono forme anche molto diverse l'una dall'altra.

Le immagini componenti questo testo sono tratte della "Gallery of fractals" di Alberto Strumia, raggiungibile tramite internet all'indirizzo http://eulero.ing.unibo.it, nelle pagine web del CIRAM - Research Centre of Applied Mathematics dell'Università di Bologna.

3. Bibliografia.