 Geometria delle Incidenze
Geometria delle Incidenze
 Condizioni di incidenza
Condizioni di incidenza
 Teorema di Desargues
Teorema di Desargues
 Teorema di Pascal
Teorema di Pascal
 Teorema di Brianchon
Teorema di Brianchon
 Dualità
Dualità
 Infinito
Infinito
 Bibliografia
Bibliografia

Configurazioni di incidenza
Se P è un punto e r una retta allora la frase
"il punto P appartiene alla retta r" (o
equivalentemente "la retta r passa per il punto
P") si dice "condizione di incidenza".
Le condizioni di incidenza non sono certamente le uniche ad essere
utilizzate in geometria: ad esempio molto importanti sono anche le
condizioni "metriche" come ad esempio "i segmenti AB
è e CD hanno la stessa lunghezza" oppure
"l'angolo ABC è di 37 gradi" cioè affermazioni
riguardanti delle quantità.
Una figura contenente rette e punti secondo certe condizioni di
incidenza si dice configurazione di incidenza. Eccone
un esempio:
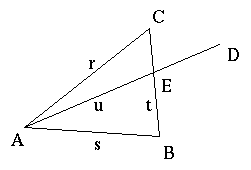 Le condizioni di incidenza che descrivono la figura sono le seguenti:
Le condizioni di incidenza che descrivono la figura sono le seguenti:
- A, B, C, D, E sono punti
- r, s, t, u sono rette
- A, B appartengono alla retta s
- B, D appartengono alla retta t
- A, C appartengono alla retta t
- A, E, D appartengono alla retta u
Teoremi di incidenza
Quando si ha a che fare con enunciati che conivolgono soltanto
condizioni di incidenza (cioè quando sia le ipotesi che la tesi
sono espresse con condizioni di incidenza) allora parliamo di
teoremi di incidenza.
Dualità
Data una certa configurazione chiamiamo configurazione duale quella
ottenuta a partire da essa cambiando i punti con le rette. Per
saperne di piú clicca qui.


Enunciato:
" Siano ABC e A'B'C' due triangoli in un piano.
Supponiamo che le rette che congiungono i vertici corrispondenti siano
tutte e tre incidenti in uno stesso punto. Allora i punti di
intersezione dei lati corrispondenti sono allineati."
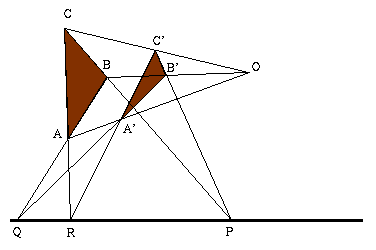 È curioso che la dimostrazione di questo teorema nel piano
non sia immediata e che invece diventi molto facile nel caso
tridimensionale: in questo caso i due triangoli appaiono come basi di
un tronco di piramide con vertice in O.
È curioso che la dimostrazione di questo teorema nel piano
non sia immediata e che invece diventi molto facile nel caso
tridimensionale: in questo caso i due triangoli appaiono come basi di
un tronco di piramide con vertice in O.
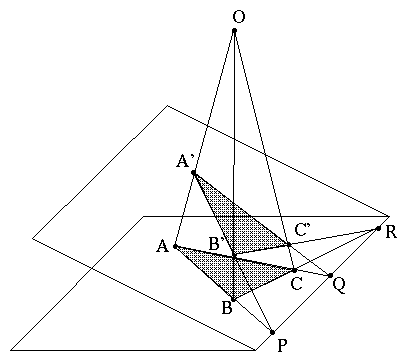 Infatti i punti P, Qe R appartengono
simultaneamente al piano contenente il triangolo ABC e quello
contenente il triangolo A'B'C' e risulteranno quindi allineati
sulla retta di intersezione dei due piani.
Infatti i punti P, Qe R appartengono
simultaneamente al piano contenente il triangolo ABC e quello
contenente il triangolo A'B'C' e risulteranno quindi allineati
sulla retta di intersezione dei due piani.
Il teorema nel caso piano può essere derivato dal caso
tridimensionale per proiezione: la configurazione di Desargues piana
può essere pensata come l'ombra di una configurazione di
Desargues tridimensionale.


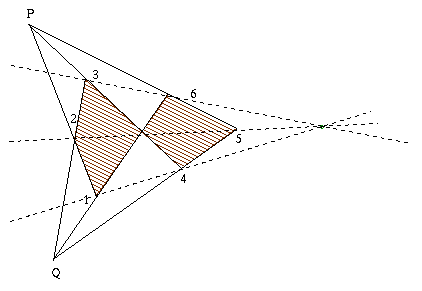
Enunciato:
" Indichiamo con
1,2,3,4,5,6, i vertici di un
esagono. Supponiamo che i vertici 1,3,5, stiano
allineati sulla retta a e che i rimanenti siano allineati sulla
retta b. Allora i tre punti di intersezione P,
Q,R dei lati opposti del triangolo sono allineati."
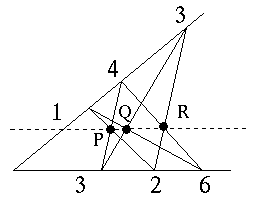 E' interessante osservare che questo teorema ha una validità
piú generale: al posto delle due rette a, b
possiamo utilizzare una conica cioè una ellisse, una iperbole,o
una parabola: in questo caso chiederemo che i 6 punti
1,2,3,4,5,6 appartengano
alla conica.
Osserviamo che le due rette incidenti possono essere pensate come caso
limite di una famiglia di iperbole: l'equazione di una iperbole
è data ad esempio da
xy = t
al variare di t otteniamo una famiglia di iperbole che
degenerano per t = 0 in due rette.
E' interessante osservare che questo teorema ha una validità
piú generale: al posto delle due rette a, b
possiamo utilizzare una conica cioè una ellisse, una iperbole,o
una parabola: in questo caso chiederemo che i 6 punti
1,2,3,4,5,6 appartengano
alla conica.
Osserviamo che le due rette incidenti possono essere pensate come caso
limite di una famiglia di iperbole: l'equazione di una iperbole
è data ad esempio da
xy = t
al variare di t otteniamo una famiglia di iperbole che
degenerano per t = 0 in due rette.


Enunciato:
" Indichiamo con 1, 2, 3, 4,
5, 6, i vertici di un esagono. Se i lati 12,
34, 56, convergono in un punto P e i lati
23, 45, 61, convergono in un punto Q
allora le tre diagonali dell'esagono 14 25 36
convergono in un punto O. "


Consideriamo le due figure qui sotto:
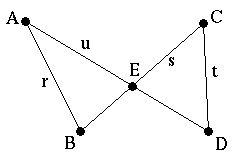
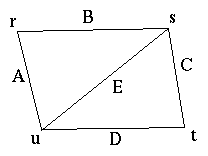 Queste figure sono legate dalla seguente relazione: sono descritte
dalle stesse condizioni di incidenza ma con il ruolo dei punti e delle
rette scambiati. Ad esempio le rette r ed
s si incontrano nel punto A nella
prima figura e nella seconda figura le i punti r ed
s sono congiunti dalla retta A.
Questa relazione va sotto il nome di
dualità.
Queste figure sono legate dalla seguente relazione: sono descritte
dalle stesse condizioni di incidenza ma con il ruolo dei punti e delle
rette scambiati. Ad esempio le rette r ed
s si incontrano nel punto A nella
prima figura e nella seconda figura le i punti r ed
s sono congiunti dalla retta A.
Questa relazione va sotto il nome di
dualità.
L'interesse principale per i fenomeni di dualità è dovuto
soprattutto al seguente fatto generale:
Principio di Dualità: "Se un certo teorema
è vero allora è vero anche il suo duale".
Il teorema di Pascal e quello di Brianchon sono duali.
Dato un teorema si può enunciare il suo duale in modo assolutamente
meccanico con una operazione quasi grammaticale.
Questo è qualcosa di piú di un semplice teorema di
geometria. Un teorema di geometria asserisce un fatto riguardante
oggetti geometrici. Il principio di dualità invece asserisce
qualcosa sui teoremi di geometria. Questo a volte viene
espresso dicendo che il principio di dualità è un
meta-teorema.


Talvolta quando due rette sono parallele diciamo che queste si
incontrano all'infinito. Questo ha significato soltanto
intuitivamente. In gemetria descrittiva si usa molto la tecnica della
prospettiva nella quale rette parallele nello spazio diventano sul
disegno rette convergenti ad un punto (che rappresenta intuitivamente
un punto all'infinito comune) chiamato fuoco.
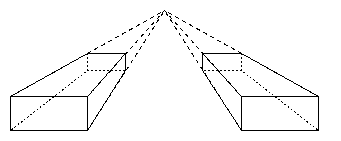
Questi concetti intuitivi possono essere resi rigorosi: oggi i
matematici usano molto spesso particolari spazi gemetrici chiamati
spazi proiettivi che rappresentano appunto lo spazio
ordinario con l'aggiunta di punti all'infinito. Ad esempio nel piano
proiettivo due rette qualsiasi si incontrano sempre. Nello spazio
tridimensionale proiettivo due rette possono essere incidenti oppure
sghembe ma non esistono rette parallele.
Ovviamente non è possibile spiegare qui come si definiscono gli
spazi proiettivi e come si possono utilizzare. Faremo perciò
semplicemente appello alla fantasia (e ad un buona dose di fede) di
chi legge. Quindi, in seguito diremo, che "r ed s si
incontrano nel punto P" o per dire che r ed s
sono realmete incidenti in un punto indicato con P oppure che
sono parallele e in questo caso diremo che un'altra retta t
passa anch'essa per P se è parallela a r (e ad
s).
Quello che a noi interessa adesso è osservare che i teoremi di
incidenza possono essere enunciati con piú efficacia con
l'utilizzo del linguaggio dei punti impropri. Per due motivi:
- Il parallelismo diventa una condizione di incidenza
- I teoremi si generalizzano comprendendo anche casi degeneri nei
quali uno o piú punti si sono allontanati all'infinito.
Ad esempio cosa succede se il punto O nel teorema di Desargues
è un punto improprio?
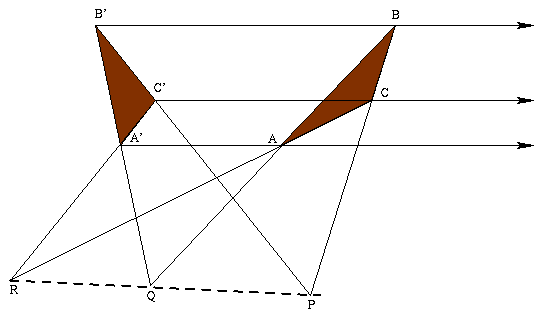 Il teorema vale anch'ora e questo caso è automaticamente
contemplato nell'enunciato che abbiamo proposto se ammettiamo che i
punti citati possano essere anche punti impropri.
Il teorema vale anch'ora e questo caso è automaticamente
contemplato nell'enunciato che abbiamo proposto se ammettiamo che i
punti citati possano essere anche punti impropri.
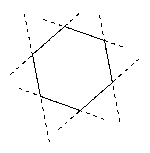
Attenzione: Cosa succede se in una configurazione
abbiamo due punti impropri? La retta che li congiunge si troverà
all'infinito cioè ogni suo punto sarà un punto
all'infinito. Questo è ad esempio quello che succede nel caso
del teorema di Pascal se l'ellisse è un cerchio e l'esagono
inscritto è regolare: i lati opposti sono paralleli e i punti di
intersezione sono allineati sulla retta all'infinito.


- R.Courant,H.Robbins
"Che cos'è la matematica?
: introduzione elementare ai suoi concetti e metodi"
Boringhieri (1971)
- D.Hilbert, S.Cohn-Vossen, P.S.Aleksandrov
"Geometria intuitiva"
Universale scientifica; 72.
Torino, Boringhieri (c1972).


 Condizioni di incidenza
Condizioni di incidenza  Teorema di Desargues
Teorema di Desargues  Teorema di Pascal
Teorema di Pascal  Teorema di Brianchon
Teorema di Brianchon  Dualità
Dualità  Infinito
Infinito  Bibliografia
Bibliografia








