Andrea Colesanti - Francesco Mugelli

Un problema isoperimetrico

Che cosa è un problema isoperimetrico? La storia del primo di questi problemi è narrata nell'Eneide. La regina Didone, in fuga da Tiro in Fenicia, approdò sulle sponde dell'attuale Tunisia e chiese al Re di quelle terre che le fosse concesso un pezzo di terra per fondarvi il proprio regno. Il Re rispose che le avrebbe dato tutta la terra che lei fosse riuscita a circondare con una pelle di bue. Didone fece tagliare la pelle a striscie sottilissime con le quali formò un filo lungo abbastanza per recintare il terreno ove fondò Cartagine.

Didone si trovò dunque ad affrontare il seguente problema:

determinare la figura piana di area massima (l'appezzamento di terreno) avendo a disposizione un perimetro fissato (la lunghezza del filo).
Questo è appunto un problema isoperimetrico.

Più in generale i problemi isoperimetrici sono quelli nei quali si chiede di trovare il dominio che rende massima una certa quantità (ad es. l'area) in una classe di domini (ad es. le figure piane) aventi tutti lo stesso perimetro.
Proviamo a risolvere un semplice problema isoperimetrico:
Tra tutti i triangoli aventi perimetro assegnato, determinare quello di area massima.
Questo problema può essere riformulato equivalentemente come:

Tra tutti i triangoli di area assegnata, determinare quello di perimetro minimo.
Non vogliamo soffermarci qui sulla equivalenza dei due problemi; speriamo che essa risulti un fatto intuitivamente spiegabile.
Risolviamo allora il problema isoperimetrico nella sua seconda formulazione.
Consideriamo un triangolo qualunque, di vertici P, Q e R; sia A il valore della sua area e sia b la lunghezza della base. L'altezza h può essere ottenuta dalla formula h = 2A/b. Riferendoci alla figura, indichiamo con x la distanza del piede dell'altezza H dal vertice Q.
Il Teorema di Pitagora ci dice che

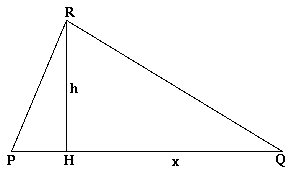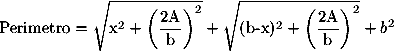
Facciamo ora scorrere il vertice R sulla retta parallela alla retta contenente il lato PQ, a distanza, 2A/b da essa, e osserviamo i corrispondenti valori della funzione perimetro. In questo tipo di movimento è il parametro x che varia e si nota che il perimetro diminuisce quando x si avvicina al valore b/2, ovvero quando il triangolo tende ad essere isoscele. In effetti si può verificare che la funzione perimetro indicata sopra, come funzione della x, ha un minimo assoluto per x = b/2.
Il risultato ottenuto può essere interpretato nel modo seguente: preso un qualunque triangolo, se ne può costruire un altro avente la stessa area, in cui uno dei lati (la base) rimane fisso e gli altri due sono uguali. Inoltre il nuovo triangolo ha perimetro minore del precedente.
Dunque, preso un qualunque triangolo di area A, che abbia due lati non uguali fra loro, se ne può costruire un altro con la stessa area e perimetro minore.

Ne segue infine che il triangolo area fissata A e perimetro minimo è il triangolo equilatero per cui vale l'uguaglianza

Per ogni altro triangolo di area A vale la disuguaglianza

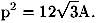
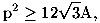
detta appunto disuguaglianza isoperimetrica.
Usando lo stesso procedimento che abbiamo descritto nel caso dei triangoli, si può provare un risultato analogo per i poligoni aventi un numero fissato di lati n:

Tra tutti i poligoni aventi n lati e area fissata A, il poligono regolare di n lati e area A ha il perimetro minimo.
In entrambi i casi che abbiamo visto, gli elementi che risolvono il problema isoperimetrico sono quelli 'più regolari', ovvero con più proprietà di simmetria, all'interno delle classi considerate. Questo fatto ci può dare uno spunto per tentare di indovinare la soluzione del seguente problema, che è il problema isoperimetrico nella sua forma più generale:
Tra tutte le figure piane di area assegnata, quale è quella di perimetro minimo?
Ci chiediamo allora, quale è la figura piana 'più regolare di tutte', ovvero con il maggior numero di assi di simmetria? Questa figura è il cerchio, ed è il cerchio infatti la soluzione del problema isoperimetrico che abbiamo appena enunciato.