In questa sezione parliamo di matematica e biologia; vedremo come una
realtà, che può essere oggetto di un esperimento scientifico
nell'ambito della biologia, possa essere descritta, o meglio "modellizzata"
in modo matematico.
Supponiamo che due popolazioni (ad esempio di microrganismi, di insetti o di
mammiferi) convivano nello stesso territorio e che interagiscano tra loro,
in modo che la crescita del numero di componenti di ciascuna popolazione
dipenda, oltre che dalla popolazione stessa, anche dall'altra.
L'interazione può avvenire in modi diversi. Vi può innanzitutto essere
cooperazione: ad esempio la prima popolazione si nutre della seconda che a sua
volta trae giovamento dalla prima in quanto questa le procura indirettamente
nutrimento.
Oppure vi può essere competizione, nel senso che le due popolazioni
lottano per avere lo stesso tipo di nutrimento. Infine vi può essere una
situazione del tipo preda-predatore, in cui una delle due popolazioni
(predatori) ha bisogno dell'altra per sopravvivere.
Indichiamo con n1(t) e n2(t) il numero di individui di ciascuna delle due popolazioni come funzioni del tempo t. La variazione della grandezza delle due popolazioni, ovvero la loro crescita o diminuzione, è data allora dalle derivate rispetto al tempo delle funzioni n1 e n2, che indichiamo con
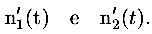
Come abbiamo detto, la variazione di ciascuna delle due funzioni n1 e n2 dipende da entrambe le popolazioni; per esprimere questo fatto in termini più matematici scriveremo una relazione che lega le derivate di n1 e n2 alle funzioni n1 e n2 stesse. Per semplificare supponiamo che la dipendenza delle derivate da n1 e n2 sia di proporzionalità:
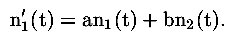
Analogamente per la derivata di n2 scriviamo
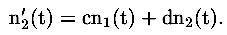
Le due relazioni che abbiamo scritto formano un sistema di equazioni
differenziali, che ha per incognite le funzioni n1 e n2.
Le equazioni differenziali rappresentano uno degli argomenti più studiati
in matematica, soprattutto nell'ambito dell'analisi matematica e della fisica
matematica.
Le costanti a, b, c e d sono i parametri del sistema; ad esse attribuiremo
valori diversi, a seconda della situazione che stiamo considerando.
Nel caso della cooperazione, ciascuna delle due popolazioni aumenta al
crescere dell'altra e dunque i coefficienti b e c avranno valori positivi.
D'altra parte, può essere ragionevole supporre che ciascuna popolazione
non abbia giovamento dall'accrescersi di sé stessa - ad esempio se vi
sono rischi di sovrappopolazione. Poniamo allora le costanti a e d minori
di zero.
Consideriamo l'esempio concreto in cui si ha
Dobbiamo studiare il sistema:
Questo sistema può essere risolto sia per via analitica (ovvero trovando esplicitamente le soluzioni) che per via numerica, ovvero utilizzando dei programmi per computer, che danno un numero finito, ma significativo, di valori numerici delle soluzioni, e ne disegnano il grafico. Se in particolare utilizziamo questo secondo metodo, troviamo i grafici riportati qui sotto:
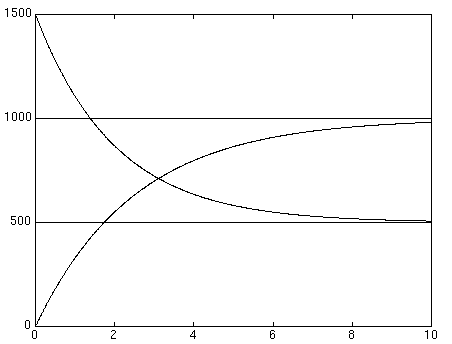
Quello che appare chiaro da questo grafico, è che, in una situazione di cooperazione, con il trascorrere del tempo il numero di individui delle due popolazioni tende ad assestarsi su valori costanti. Tali valori dipendono dai parametri del sistema, ma anche dai cosiddetti "dati iniziali", ovvero dal numero di individui che componevano le due popolazioni all'inizio dell'esperimento.
Consideriamo ora il caso in cui le due popolazioni siano in competizione; i parametri del sistema devono essere modificati. Ciascuna delle due popolazioni è svantaggiata dall'aumentare dell'altra, e trae invece giovamento dal proprio accrescersi, in quanto un maggior numero di individui la rende più forte nella competizione. Per fare un esempio concreto, consideriamo il sistema seguente, ottenuto dal sistema iniziale ponendo
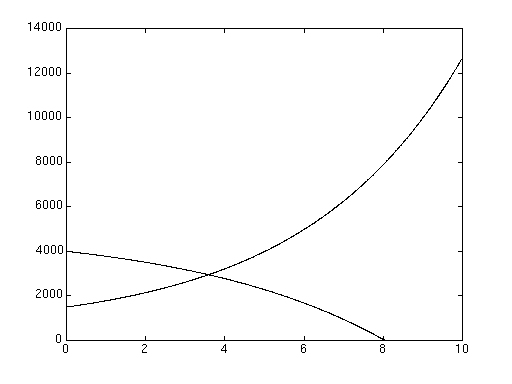
Come si vede, in caso di competizione, una delle due popolazioni si estingue in un tempo finito t0, mentre l'altra cresce liberamente da t0 in poi. Quale delle due popolazioni si estingua ed il tempo di estinzione t0, sono eventi dipendenti ancora una volta dai parametri del sistema e dai valori iniziali.
Veniamo infine alla situazione preda-predatore. In questo caso assumiamo che la popolazione delle prede, n1, decresca rispetto al numero n2 dei predatori, e cresca invece ripsetto al numero delle prede stesse; dunque poniamo a > 0 e b < 0. Per quanto riguarda invece la popolazione dei predatori, questa cresce con il crescere delle prede, d > 0, ma decresce con l'aumentare dei predatori stessi, poiché vi è maggiore competizione tra i predatori, dunque c < 0. Analizziamo l'esempio specifico:
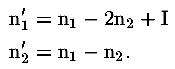
Il termine I, positivo, rappresenta una immigrazione, costante nel tempo, di prede nel territorio dell'esperimento; questo serve a rendere più completo il nostro modello. Riportiamo qui il grafico che ci dà l'andamento di n1 e n2 nel tempo, per un valore di I=1500, e per valori iniziali di n1(0)=2500 e n2=2000.
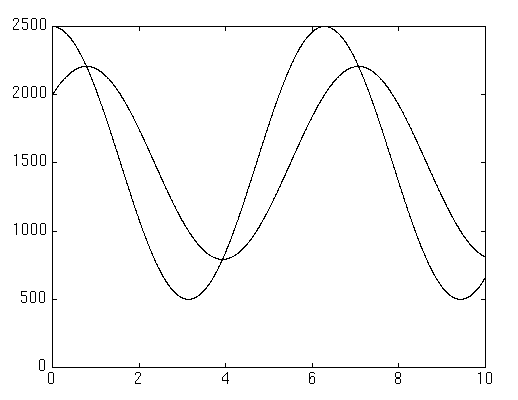
Come si vede il sistema ha un comportamento "periodico", ovvero n1 e n2 sono funzioni periodiche sfasate nel tempo l'una rispetto all'altra. Ciò significa che le prede e i predatori crescono e decrescono, in momenti diversi, ciclicamente.