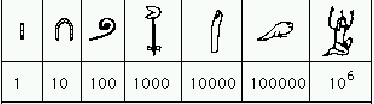
Egizi - geroglifica
numerazione a base decimale, additiva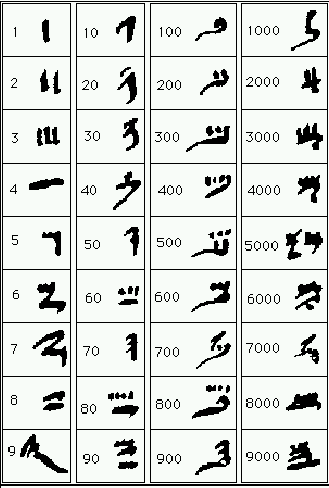
I documenti per ricostruire la matematica pre-greca a disposizione degli studiosi sono piuttosto scarsi e si limitano a qualche papiro e all'analisi di fonti indirette come le opere di architettura, le iscrizioni, le arti figuative.
Il più famoso e completo testo matematico a noi noto è il papiro di Rhind che risale al 1650 a.C., copia - avverte lo scriba Ahmes - di un esemplare più antico di due secoli. All'inizio del papiro si legge:
Regole per scrutare la natura e per conoscere tutto ciò che esiste, ogni mistero, ogni segretoe contiene tavole di calcolo e 87 problemi ripartiti in vari gruppi, di natura pratica connessi con le attività di ingegneria edile, di agricoltura, di amministrazione, di approvigionamento etc., esposti con intento didattico.
Il papiro è scritto in ieratico, la scrittura corsiva egizia, usata per scrivere con pennello e inchiostro sui papiri, che si diffonde dal 2400 a.C. circa accanto alla più antica scrittura monumentale geroglifica.
Il sistema di numerazione egizio è di tipo additivo con base decimale. Nella scrittura geroglifica, usata per iscrizioni su lapidi e monumenti, i numeri vengono rappresentati tramite la giustapposizione di sette simboli rappresentanti le potenze di 10, da 1 a 1000000. Non esiste lo zero, né come segno né come spazio vuoto. Uno dei più antichi reperti con numeri scritti in geroglifici è la cosiddetta mazza del faraone Narmer (3000 a.C. circa) che commemora la conquista delle regioni del delta del Nilo e in cui sono riportati alcuni grandi numeri.
Nella scrittura ieratica i simboli si semplificano notevolmente e si formano nuovi simboli per indicare simboli ripetuti. I segni usati sono ora più numerosi, ma permettono una scrittura più rapida dei numeri.
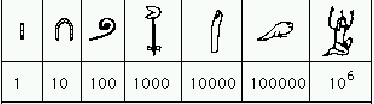 |
Egizi - geroglificanumerazione a base decimale, additiva |
 |
Egizi - ieraticanumerazione a base decimale, additiva |
Nei testi matematici egizi troviamo quelle che noi chiameremmo frazioni unitarie, cioè di tipo 1/n con n intero positivo, a cui si aggiunge la frazione particolare 2/3. Nella scrittura geroglifica le frazioni unitarie venivano rappresentate ponendo sopra il numero che per noi è il denominatore, cioè quello che indica in quante parti si deve dividere, il simbolo della bocca, simbolo che sembra legato al problema della spartizione del cibo. Per la frazione 1/2 e la frazione 2/3 si usavano simboli speciali.

Nella scrittura ieratica il simbolo della bocca è sostituito da un semplice punto ed aumenta il numero delle frazioni per cui si ricorre a simboli speciali: 1/3, 1/4 e 1/6 oltre a 1/2 e 2/3.
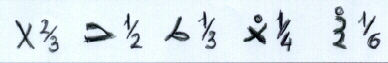
Il concetto generale di frazione sembra sia rimasto estraneo agli egizi. Una frazione che noi scriveremmo come p/q (con p e q interi positivi), e che poteva venir fuori nel corso di problemi o procedimenti, veniva espressa come somma di un intero e di frazioni unitarie. Ad esempio nel papiro di Rhind 19/8 è scritto come 2+1/4+1/8.
Non è chiaro secondo quali criteri si sceglieva una scomposizione piuttosto che un'altra. Nel Papiro di Rhind si trova una tabella che dà le scomposizioni delle frazioni del tipo ![]() con n dispari da 5 a 101 chiedendo: ``quale parte di
con n dispari da 5 a 101 chiedendo: ``quale parte di ![]() è 2?''. Le scomposizioni, fornite senza spiegazione, hanno alcune caratteristiche comuni: non compaiono mai termini ripetuti, quindi ad esempio
è 2?''. Le scomposizioni, fornite senza spiegazione, hanno alcune caratteristiche comuni: non compaiono mai termini ripetuti, quindi ad esempio ![]() non è
non è ![]() ma
ma ![]() , i denominatori sono in ordine crescente, i termini sono al massimo quattro e in generale nel numero minimo possibile rispettando la prima condizione. Altrove anche la frazione
, i denominatori sono in ordine crescente, i termini sono al massimo quattro e in generale nel numero minimo possibile rispettando la prima condizione. Altrove anche la frazione ![]() è ammessa come fondamentale nelle scomposizioni.
è ammessa come fondamentale nelle scomposizioni.
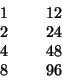

Ovviamente è possibile trovare esattamente il dividendo solo se la divisione è esatta. In caso contrario si può ottenere il quoziente intero approssimato trovando l'intero minore ma più vicino possibile al dividendo.
Ma si può anche trovare il risultato esatto servendosi delle frazioni introducendo dopo le duplicazioni, quando le somme parziali superano il dividendo, le divisioni per due, (o comunque una successione di divisioni). Dovendo ad esempio eseguire ![]() nel Papiro di Rhind si procede così:
nel Papiro di Rhind si procede così:
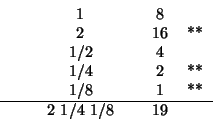
|
|
|
|
|