L'addizione veniva effettuata già in India in maniera molto simile a quella odierna; l'idea fondamentale è quella dell'incolonnamento e l'esecuzione delle somme a partire dalla colonna delle unità con eventuale riporto. Nel Liber abaci e in molti trattati d'abaco il risultato veniva però scritto sopra e non sotto gli addendi.
Per la sottrazione accanto ad un procedimento che è sostanzialmente il nostro, troviamo anche un modo detto per complemento; consiste nel sommare a partire dalla colonna delle unità la cifra del minuendo con il complemento a 10 della cifra del sottraendo nella stessa colonna e, scritte le unità del risultato, procedere poi analogamente con la colonna subito a sinistra con l'accorgimento che se la somma parziale trovata nella colonna precedente non supera 10 si deve calcolare non il complemento a 10 ma il complemento a 9.
La moltiplicazione è l'operazione per la quale troviamo la maggior varietà di metodi, che anche graficamente assumono aspetti molto diversi tra loro e ai quali gli abachisti assegnarono i nomi più fantasiosi. L'attuale metodo veniva detto in Toscana per biricucolo forse dal nome di certe crostate di albicocche che lo schema a quadretti presente nei testi più antichi poteva ricordare. Probabilmente per lo stesso motivo lo stesso metodo veniva invece indicato come per schacchiere a Venezia e per organetto a Verona. Si tratta comunque di un metodo molto antico, già usato in India, che a lungo fu solo uno dei tanti non meno agevoli utilizzati.
Nel Liber abaci Fibonacci espone un metodo detto per crocetta noto agli indiani come moltiplicazione fulminea perché, una volta acquisito, è un metodo molto rapido tanto che viene ancora oggi usato dai campioni di calcolo mentale.
Un algoritmo che riduce al minimo le possibilità di errori perché i possibili riporti si hanno solo in sede di addizioni che seguono una serie di semplici moltiplicazioni a una cifra è quello detto in Italia come a gelosia e noto già agli indiani e poi agli arabi come a caselle o a reticolo. Nel procedimento moltiplicando e moltiplicatore si scrivono lungo due dei lati di un rettangolo diviso in caselle a loro volta divise a metà lungo la diagonale entro cui si scrivono decine e unità dei prodotti incrociati delle singole cifre di moltiplicando e moltiplicatore e poi si somma lungo le diagonali.
Gelosia è il nome della grata posta a protezione delle finestre e dunque, come si legge ad esempio nel trattato di Francesco Feliciano, Scala grimaldelli
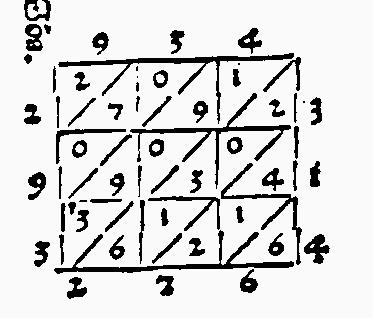
Moltiplicar per gelosia over per graticola si è per certa similitudine di quelle che si mettono alli balconi, over finestre, perché le donne non si vedano s'elle non vogliono. Il qual si fa al modo del quadrilatero, eccetto che a quello si teneva le decene, e a questo non si tiene. Ma ogni cosa si mette giù, fatto la figura, come vedi qui da canto.Ecco uno schema di moltiplicazione a gelosia, tratto dall'Aritmetica di Treviso. La moltiplicazione eseguita è 934 per 314, (da porre in alto e a destra della griglia) il cui risultato, 293276, si legge di seguito al margine sinistro e basso della griglia stessa:
Il quadrilatero era un altro metodo molto comune, esposto anche nel Liber abaci. Questo è lo schema relativo alla stessa moltiplicazione precedente, tratto sempre dall'Aritmetica di Treviso:
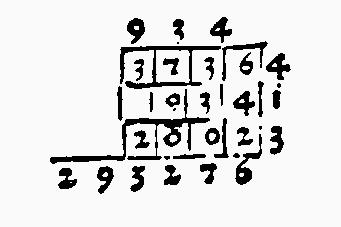
Fra i molti altri ricordiamo ancora un metodo alla francese detto anche a calice o coppa o tazza o bicchiere per la forma dello schema, rovesciato rispetto a quello che viene altrove indicato come a piramide.
Prova tu
Per quanto riguarda la divisione, il procedimento che noi utilizziamo ha raggiunto l'attuale forma nel XV secolo ed è detto a danda probabilmente perché una volta ottenuta una cifra del quoziente il dividendo deve dare una cifra da collocare accanto al precedente resto. Si trovano, e tuttora si insegnano, due varianti, a danda lunga e a danda corta a seconda che si scriva o no la sottrazione che porta di volta in volta al resto.
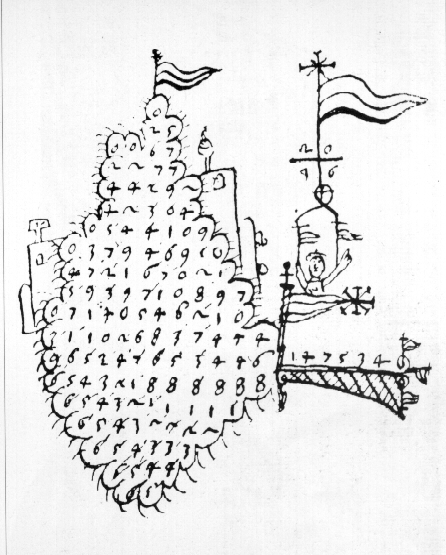
Prima del XV secolo la divisione veniva eseguita con un metodo di origine indiana che gli abachisti medioevali chiamavano a galera o a battello per la somiglianza che vedevano nella disposizione delle cifre nello schema risolutivo con una nave a remi. Questo metodo anche se più laborioso e meno sicuro della danda venne usato fino al XVII secolo.