Il giardino di Archimede  Un museo per la matematica

Breve storia della trigonometria

I logaritmi. Un impulso decisivo allo sviluppo delle tecniche trigonometriche viene dall'invenzione dei logaritmi da parte di JOHN NAPIER (NEPERO, 1550-1617), mediante i quali venivano drasticamente semplificati i calcoli: le moltiplicazioni e le divisioni si riducevano a somme e sottrazioni, le potenze ed estrazioni di radici a prodotti e quozienti per un intero. Ci si accorse ben presto che anche i calcoli trigonometrici potevano essere fortemente semplificati da un uso combinato delle tavole delle funzioni circolari e di quelle logaritmiche. Ad esempio la risoluzione di un triangolo dati un lato e gli angoli, per la quale si usa il teorema dei seni: $$b = \frac{a \mathop{\rm sen}\nolimits \, \beta}{\mathop{\rm sen}\nolimits \, \alpha}$$ poteva essere semplificata prendendo i logaritmi: $$\log b = \log a + \log \mathop{\rm sen}\nolimits \, \beta - \log \mathop{\rm sen}\nolimits \, \alpha,$$ dato che invece di una moltiplicazione e una divisione si doveva fare una somma e una sottrazione. Di qui lo sviluppo della trigonometria in due direzioni: da una parte occorrevano delle tavole che per ogni angolo riportassero direttamente il logaritmo del seno e delle altre funzioni trigonometriche, in modo da non dover prima cercare il seno nelle tavole trigonometriche, e poi il suo logaritmo in quelle logaritmiche. In altre parole, alle tavole usuali dei seni e delle altre funzioni circolari si aggiungono quelle dei loro logaritmi, giungendo così a tavole logaritmico-trigonometriche. D'altra parte, perché queste tavole potessero essere usate col massimo profitto, occorreva servirsi di formule trigonometriche che contenessero solo somme e sottrazioni (nel qual caso non c'era bisogno di logaritmi), o solo moltiplicazioni e divisioni, che con l'uso dei logaritmi venivano ricondotte alle prime. Al contrario formule miste, nelle quali comparivano cioè sia somme che prodotti, erano meno pratiche perché non era possibile ridurle alle sole somme e sottrazioni. C'è allora per ogni problema la ricerca di una forma di formule risolutive che permettessero l'uso dei logaritmi. Ad esempio, nella risoluzione di un triangolo dati i lati, la formula di Carnot $$\cos \, \alpha= \frac{b^{2}+c^{2}-a^{2}}{2bc}$$ non è calcolabile per mezzo dei logaritmi, e dunque è preferibile la formula di Briggs 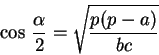$$\cos \, \frac{\alpha}{2} = \sqrt{\frac{p(p-a)}{bc}}$$ che prendendo i logaritmi diventa $$\log \cos \, \frac{\alpha}{2} = \mbox{$\frac{1}{2}$} \log p +... ...- \mbox{$\frac{1}{2}$} \log b - \mbox{$\frac{1}{2}$} \log c.$$ Inutile dire che l'avvento delle macchine calcolatrici ha reso praticamente inutili queste precauzioni, dato che con esse fare un prodotto non è più complicato che fare una somma.

Indice: breve storia della trigonometria

Pagina successiva

Pagina precedente

Pagina principale