- ... Pisano 1
- Leonardo era figlio di Bonaccio, un funzionario del comune di Pisa; da ``Fi' Bonacci'' (figlio di Bonaccio) viene Fibonacci, altro nome sotto cui è noto.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Pisa 2
- vedi Arrighi, op. cit.; B. Casini, Il catasto di Pisa del 1428-29, Tip. Ed. Giardini, Pisa, 1964
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cose. 3
- vedi l'Appendice testi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... moderno. 4
- In Appendice attività si trova un possibile esempio di semplice scheda di lavoro su queste prime pagine
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... superficiali. 5
- I sottomultipli lineari della pertica sono piede, oncia, punto (``li 2 punti sono di grossesa di uno granello di grano'') con questi rapporti: 1 pertica = 6 piedi, 1 piede = 18 once, 1 oncia = 18 punti. Nel caso di misure superficiali si usa la pertica superficiale (pertica
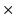 pertica) detta anche semplicemente di nuovo pertica, e vari multipli e sottomultipli
pertica) detta anche semplicemente di nuovo pertica, e vari multipli e sottomultipli
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distinzioni. 6
- La Pratica geometriae è così strutturata: a una parte di Introductoria seguono otto distinctiones: 1. De multiplicatione latitudinum camporum quadratorum rectos angulos habentium in eorum longitudine, in quibus multiplicationibus eorum embada continentur; 2. De invenctione radicum; 3. In mensuratione omnium camporum: trianguli, quadrilateri, multilateri, circuli et eorum portiones et obliquae figurae et commixtae ex rectis et curvis lineis, campi qui in ascensione montium iacent; 4. De divisione camporum inter consortes: trianguli, quadrilateri, multilateri, circuli; 5. De radicibus cubicis inveniendis; 6. In dimensione corporum; 7. De inventione altitudinum rerum elevatarum et profunditatum atque longitudinum planitierum; 8. De quibusdam subtilitatibus geometricis
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... calcolo.7
- Per quanto riguarda l'uso e la storia di alcuni strumenti usati nelle geometrie pratiche si veda anche [3]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... modo:8
- Leonardo Pisano si riferisce in realtà al modo usato da alcuni per misurare in un bosco gli alberi adatti per le navi. Vedi Appendice testi^.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... comprensione. 9
- vedi Appendice testi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... avanti) 10
- Notare che il dover compiere due aggiustamenti simultanei equivale in qualche modo a trattare due incognite ``sul campo''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dell'asta.11
- Poteva essere utilizzato come ulteriore variante nel caso 1, dove non esistono limitazioni sul posizionamento.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ghovito12
- Il gomito, o anche cubito, è un'unità di misura corrispondente a circa 44 cm, la distanza tra il gomito e l'estremità del dito medio
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... problema? 13
- Una soluzione:
Puoi trovare
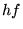 usando la similitudine dei triangoli
usando la similitudine dei triangoli 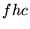 e
e 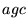 :
:
Di queste misure
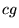 è la tua distanza dal bastone, che puoi misurare
è la tua distanza dal bastone, che puoi misurare
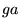 è quanto il bastone è più alto di te, che puoi misurare
è quanto il bastone è più alto di te, che puoi misurare
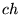 è la tua distanza dalla torre, che devi misurare
è la tua distanza dalla torre, che devi misurare
Conosciute le precedenti misure puoi trovare 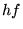 risolvendo la proporzione:
risolvendo la proporzione:
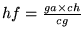 . Ad
. Ad 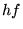 devi aggiungere poi
devi aggiungere poi 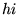 , cioè la tua altezza.
, cioè la tua altezza.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... calcolo. 14
- Una soluzione guidata - caso 1
Misurazione dell'altezza di ..................
Strumento utilizzato:.................................
Descrizione della fase di misurazione:
Misure occorrenti:
- la tua altezza-occhi
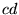 =...
=...
- l'altezza dell'asta che utilizzi
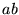 =...
=...
- la tua distanza dall'asta
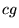 =...
=...
- la tua distanza dall'oggetto di cui vuoi conoscere l'altezza
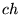 =...
=...
Disegno schematico della situazione:
Vale la proporzione
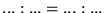 in cui
in cui
perciò
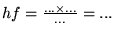 .
.
Infine 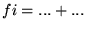 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elementare)15
- Un altro modo di presentare il caso 2 può essere quello di dare un'interpretazione delle proporzioni in termini di unità di misura. Facendo ben osservare il disegno
si può tentare di illustrare il procedimento di Cristofano spiegando ad esempio che
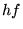 fa da unità di misura alle distanze torre-osservatore tanto quanto l'unità di misura ``concreta'' che abbiamo scelto (il nostro ``metro'' o il ``braccio'' che è posto anche sull'asta) fa per le distanze asta-osservatore.
In altre parole possiamo dire che io - osservatore - ho a disposizione per fare le misure il mio metro-braccio e per me conoscere una misura significa conoscerla in metri o braccia; immaginiamo poi che invece qualcun altro - magari un gigante - abbia a disposizione come unità di misura il pezzo
fa da unità di misura alle distanze torre-osservatore tanto quanto l'unità di misura ``concreta'' che abbiamo scelto (il nostro ``metro'' o il ``braccio'' che è posto anche sull'asta) fa per le distanze asta-osservatore.
In altre parole possiamo dire che io - osservatore - ho a disposizione per fare le misure il mio metro-braccio e per me conoscere una misura significa conoscerla in metri o braccia; immaginiamo poi che invece qualcun altro - magari un gigante - abbia a disposizione come unità di misura il pezzo 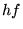 della torre. Quello che io vorrei scoprire è quanto vale l'unità-torre del gigante rispetto alla mia. Come fare?
Io e il gigante ci posizioniamo in
della torre. Quello che io vorrei scoprire è quanto vale l'unità-torre del gigante rispetto alla mia. Come fare?
Io e il gigante ci posizioniamo in 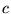 . Osserviamo che se io misuro la mia distanza dall'asta, cioè
. Osserviamo che se io misuro la mia distanza dall'asta, cioè 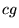 , e il gigante misura la sua distanza dalla base della torre, cioè
, e il gigante misura la sua distanza dalla base della torre, cioè 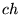 (per lui il fiume non è un ostacolo: può scavalcarlo con un solo passo!), otteniamo lo stesso valore, ovviamente ciascuno nella propria unità di misura (questo è il miracolo della similitudine). Se ora anche io potessi misurare con il mio metro la distanza
(per lui il fiume non è un ostacolo: può scavalcarlo con un solo passo!), otteniamo lo stesso valore, ovviamente ciascuno nella propria unità di misura (questo è il miracolo della similitudine). Se ora anche io potessi misurare con il mio metro la distanza 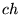 misurata dal gigante scoprirei quanto vale la sua unità di misura; infatti se ad esempio la sua misurazione avesse dato il valore 3 e la mia 30 vorrebbe dire che la sua unità-torre è 10 volte più grande della mia. Purtroppo, mentre nel caso precedente potevo misurare
misurata dal gigante scoprirei quanto vale la sua unità di misura; infatti se ad esempio la sua misurazione avesse dato il valore 3 e la mia 30 vorrebbe dire che la sua unità-torre è 10 volte più grande della mia. Purtroppo, mentre nel caso precedente potevo misurare 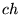 , e avrei subito scoperto quanto l'unità-torre del gigante è più grande della mia, in questo caso, a causa del fiume, devo ricorrere a qualche altro ``trucco''.
Se io e il gigante ci spostiamo in
, e avrei subito scoperto quanto l'unità-torre del gigante è più grande della mia, in questo caso, a causa del fiume, devo ricorrere a qualche altro ``trucco''.
Se io e il gigante ci spostiamo in 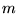 (o in un qualsiasi altro punto) e ripetiamo le misurazioni come sopra queste risultano sempre coincidenti, cioè la mia misura di
(o in un qualsiasi altro punto) e ripetiamo le misurazioni come sopra queste risultano sempre coincidenti, cioè la mia misura di 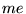 e la sua di
e la sua di 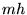 hanno lo stesso valore. Questo ancora non è risolutivo perchè quello di cui avrei bisogno per scoprire quanto vale l'unità-torre è di poter misurare con il mio metro una distanza di cui conosco il valore del gigante, cioè confrontare le due misurazioni di una stessa lunghezza. Quale potrebbe essere questa lunghezza?
Trovato! È
hanno lo stesso valore. Questo ancora non è risolutivo perchè quello di cui avrei bisogno per scoprire quanto vale l'unità-torre è di poter misurare con il mio metro una distanza di cui conosco il valore del gigante, cioè confrontare le due misurazioni di una stessa lunghezza. Quale potrebbe essere questa lunghezza?
Trovato! È 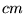 , cioè di quanto ci siamo spostati tra il primo e il secondo posizionamento. Infatti con il metro io posso misurarla senza problemi, infatti il fiume questa volta non mi dà noia; dunque posso conoscere la misura di
, cioè di quanto ci siamo spostati tra il primo e il secondo posizionamento. Infatti con il metro io posso misurarla senza problemi, infatti il fiume questa volta non mi dà noia; dunque posso conoscere la misura di 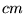 in metri tramite misurazione diretta. D'altra parte
in metri tramite misurazione diretta. D'altra parte 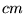 è anche la differenza tra
è anche la differenza tra 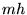 e
e 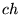 di cui conosco la misura in unità-torre (uguali rispettivamente alle mie di
di cui conosco la misura in unità-torre (uguali rispettivamente alle mie di 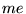 e
e 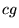 ); dunque posso calcolare la misura di
); dunque posso calcolare la misura di 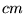 in unità-torre tramite sottrazione. Ecco che non mi resta che confrontare le due misure di
in unità-torre tramite sottrazione. Ecco che non mi resta che confrontare le due misure di 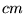 ; in particolare dividendo la misura in metri per quella in unità-torre scopro quanti metri ci vogliono per fare un'unità-torre. In altre parole ho in definitiva trovato la misura di
; in particolare dividendo la misura in metri per quella in unità-torre scopro quanti metri ci vogliono per fare un'unità-torre. In altre parole ho in definitiva trovato la misura di 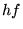 in metri e per avere l'altezza dell'intera torre devo solo aggiungerci l'altezza dei miei occhi (
in metri e per avere l'altezza dell'intera torre devo solo aggiungerci l'altezza dei miei occhi (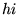 ). (In totale ho compiuto 3 misurazioni e ho dovuto fare 3 operazioni aritmetiche.)
). (In totale ho compiuto 3 misurazioni e ho dovuto fare 3 operazioni aritmetiche.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
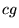 è la tua distanza dal bastone, che puoi misurare
è la tua distanza dal bastone, che puoi misurare
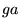 è quanto il bastone è più alto di te, che puoi misurare
è quanto il bastone è più alto di te, che puoi misurare
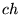 è la tua distanza dalla torre, che devi misurare
è la tua distanza dalla torre, che devi misurare
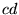 =...
=...
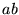 =...
=...
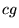 =...
=...
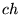 =...
=...
![]() in cui
in cui
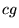 =...
=...
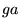 =...
=...
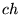 =...
=...