Propagazione degli errori

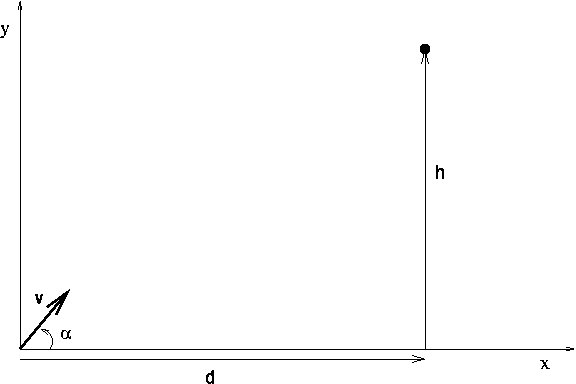
L'altezza raggiunta dal proiettile alla distanza $d$ è data da

$$h=\tan\alpha \cdot d -\frac{gd^2}{2v^2\cos^2\alpha}$$

Per la formula di propagazione degli errori

$$\sigma^2(h)\simeq \left( \frac{d}{\cos^2\alpha} - \frac{gd^2\sin\... ...^2 \sigma^2_{\alpha} + \left(\frac{gd^2}{v^3\cos^2\alpha} \right)^2 \sigma^2_v$$

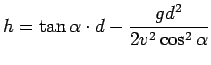
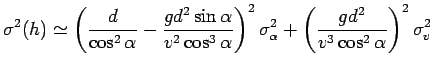
L'approssimazione consiste nell'assumere un andamento lineare della funzione nell'intorno di $\hat{v}$ e $\hat{\alpha}$, ovvero si approssima

$$\Delta h = h(\hat{v} + \sigma_v) - h(\hat{v} - \sigma_v)$$

con

$$\Delta_0 h = 2 \left. \frac{\partial h}{\partial v}\right\vert _{\hat{\alpha},\hat{v}} \sigma_v$$

(e analogamente per $\alpha$)

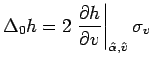
Possiamo dunque valutare la bontà dell'approssimazione tramite

$$\vert(\Delta h - \Delta_0 h)/\Delta h \vert$$

Implementiamo le funzioni in R:

g = 9.8
alphahat = acos(-1)/4
vhat = 100
d=500

ybal <- function(x,alpha=alphahat,v=vhat) {
tan(alpha) * x - g/2*x^2/(v^2*cos(alpha)^2)
}

dybal <- function(alpha=alphahat,v=vhat,dalpha,dv,x) {
 sqrt(((x-g*x^2*sin(alpha)/(cos(alpha)*v^2))/(cos(alpha)^2)*dalpha) ^2 +
    (g*x^2/(cos(alpha)^2*v^3)*dv) ^2)
}

approx =  function(alpha=alphahat,v=vhat,dalpha,dv) {
 dy = abs(ybal(alpha=alpha+dalpha,v=v+dv,x=d)-
          ybal(alpha=alpha-dalpha,v=v-dv,x=d))
 dys = 2*dybal(alpha=alpha,dalpha=dalpha,v=v,dv=dv,x=d)
 abs((dy-dys)/pmax(dy,0.0001))
}

alphapprox =function(x,alpha=alphahat,v=vhat) {
 approx(alpha=alpha,v=v,dalpha=x,dv=0)
}
vapprox =function(x,alpha=alphahat,v=vhat) {
 approx(alpha=alpha,v=v,dalpha=0,dv=x)
}

Dai grafici

curve(alphapprox(x),0,0.4)
curve(vapprox(x),0,50)

possiamo valutare che un'approssuimazione migliore del 10 % si avrà per

$$\sigma_{\alpha} <\sim 0.3  rad$$

$$\sigma_{v} <\sim 20  m/s$$

Possiamo verificare questi risultati tramite una simulazione:

simbali <- function(dalpha,dv,n=10000,alpha=alphahat,v=vhat,x=d) {
# generiamo un vettore con n valori di h
 asam = rnorm(n,mean=alpha,sd=dalpha)
 vsam = rnorm(n,mean=v,sd=dv)
 hsam = ybal(alpha=asam,v=vsam,x=x) 

# media e varianza attesi:
 yexp = ybal(alpha=alpha,v=v,x=x)
 dyexp = dybal(alpha=alpha,dalpha=dalpha,v=v,dv=dv,x=x)

# confronto fra distribuzione simulata e 
# distribuzione attesa nell'appros. lineare
 binsize = dyexp/5 
 curve(dnorm(x,mean=yexp,sd=dyexp)*binsize*n,
       yexp-5*dyexp,yexp+5*dyexp,col="red")
 hist(pmax(hsam,yexp-10*dyexp),
      breaks=seq(yexp-10*dyexp,yexp+10*dyexp,binsize),add=T)
}

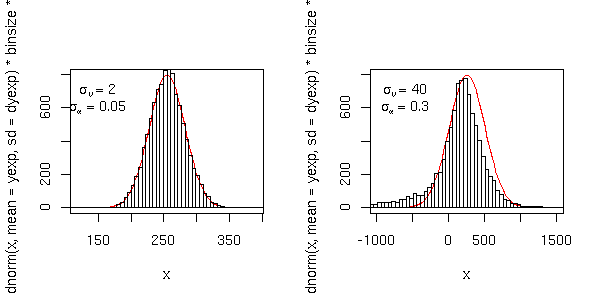
Nel caso in cui è valida l'approssimazione lineare, ad esempio

simbali(dalpha=0.05,dv=2)

ci aspettiamo che la distribuzione di $h$ sia una gaussiana, la cui varianza è ottenuta dalla formula di propagazione. Per valori di $\sigma_{\alpha}$ o $\sigma_{v}$ superiori ai limiti dati ci aspettiamo evidenti differenze sia nel valore atteso che nella varianza, ad esempio:

simbali(dalpha=0.3,dv=40)