Convoluzione di funzioni densità

Convoluzione di due distribuzioni uniformi

Dalla formula di convoluzione di Gauss si ha

$$g(y) = \int_{a}^b \frac{1}{(b-a)}f_x(y-x)dx = \int_{max(a,y... ...{2b-y}{(b-a)^2} & a+b < y < 2b 0 & y>2b \end{array} \right.$$

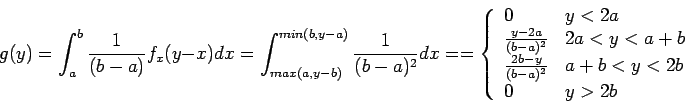
Si ottiene cioè una funzione triangolare che possiamo implementare in R :

hy <- function(y,a=-1,b=1) {
out=c()
for (i in 1:length(y)) {
 out[i]=0
 if (y[i] > 2*a & y[i] < 2*b) { 
  if (y[i] < (a+b)) 
   out[i]=(y[i]-2*a)/(b-a)^2
  else 
   out[i]=(2*b-y[i])/(b-a)^2
 }
}
out
}

(Si noti che la funzione, per poter essere disegnata con le funzioni plot o curve, deve poter agire su un vettore y di lunghezza arbitraria. Un'alternativa all'uso del ciclo for è l'operatore ifelse che può ritornare un vettore.)

Possiamo adesso visualizzare la funzione e verificare che riproduce la distribuzione di un campione ottenuto dalla somma di due variabili generate in modo uniforme fra $a$ e $b$:

mya=-1
myb=1
n=10000
sample = runif(n,min=mya,max=myb) + runif(n,min=mya,max=myb)
deltax=(myb-mya)/20
hist(sample, breaks=seq(2*mya-1,2*myb+1,deltax))
curve(hy(x,a=mya,b=myb) * n * deltax, add=T, col="red")

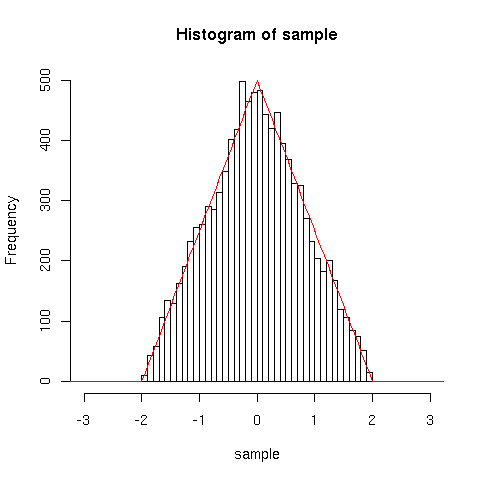
Si noti il fattore $n * deltax$ necessario per normalizzare correttamente la funzione densità di probabilità alla distribuzione del campione.

Convoluzione di una funzione densità gaussiana e una esponenziale

Si supponga di misurare il tempo di decadimento di un nucleo radioattivo con un apparato dotato di risoluzione temporale $\sigma$, ovvero tale che l'errore nella misura possa essere descritto con una gaussiana di valore atteso nullo e deviazione standard $\sigma$:

$$t' = t + \epsilon$$

Le funzioni densità di probabilità di $t$ e $\epsilon$ sono dunque

$$f(t)=\frac{1}{\tau}\exp(-t/\tau)$$

$$g(\epsilon)=\frac{1}{\sqrt{2\pi} \sigma}\exp(-\epsilon^2/\sigma^2)$$

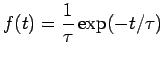
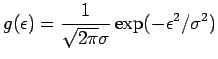
Vogliamo scrivere con R la funzione densità per la variabile $t'$

$$h(t') = \int^{\infty}_{-\infty}g(\epsilon) f(t'-\epsilon) d\epsil... ...u} \int^{t'}_{-\infty} g(\epsilon) \frac{\exp(\epsilon/\tau)}{\tau} d\epsilon$$

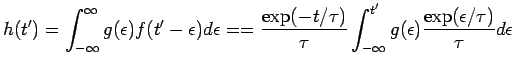
In questo caso la funzione convoluta non è calcolabile analiticamente. Dobbiamo dunque risolvere l'integrale numericamente utilizzando la funzione integrate di R.

fee <- function(e,tau,sigma) {
 dnorm(e,sd=sigma)* exp(e/tau)/tau
}

expconv <- function(t,tau,sigma) {
 out=c()
 for (i in 1:length(t)) {
  out[i] = exp(-t[i]/tau) * 
    integrate(fee,-6*sigma,t[i],sigma=sigma,tau=tau)$value
 }
 out
}

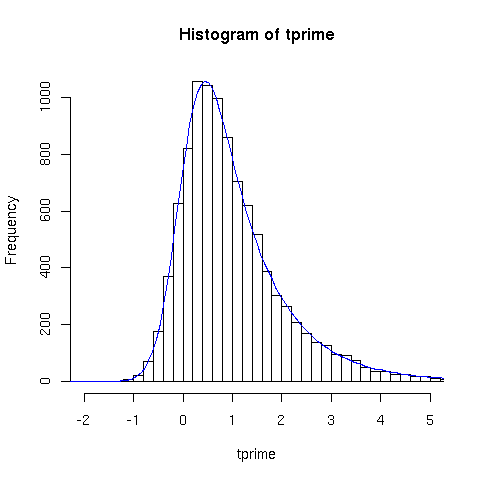
Possiamo adesso simulare un campione e verificare la correttezza della distribuzione densità calcolata

n=10000
tau=1
sigma=0.4
t=rexp(n,rate=1/tau)
eps=rnorm(n,sd=sigma)
tprime=t+eps
deltax=0.2
hist(tprime,breaks=seq(-10,20,deltax),xlim=c(-2,5)) 
curve(expconv(x,tau=tau,sigma=sigma)*n*deltax,add=T,col="blue")