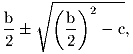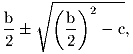
L'intestazione del problema dice: "Esempio del terzo dei casi composti".
Che cosa significa?

Le quantità che Pacioli usa sono sempre positive.
Se noi dunque possiamo indicare una generica equazione di secondo grado come x² + bx + c = 0 (che comprende sia x² + 3x - 7 = 0 che x² - 3x + 7 = 0 che x² - 7 = 0 eccetera), Pacioli ha invece bisogno di distinguere vari casi a seconda delle possibili combinazioni dei segni e della eventuale presenza di coefficienti nulli.
Troviamo allora tre casi "semplici", corrispondenti alle equazioni che noi potremmo scrivere così (con b e c positivi):

e tre casi "composti", corrispondenti a:

Il problema che abbiamo scelto rientra nell'ultimo caso.
Poco sopra, Pacioli aveva enunciato la "regola" per risolvere l'equazione in ciascun caso. Quello che per noi è rappresentato dalla formula risolutiva, che per la nostra equazione x² + c = bx scriveremmo