A Museum for Mathematics
| The Garden of Archimedes
A Museum for Mathematics |
| integration
and measure |
| from Cauchy
| from
Riemann | from Peano
| from
Jordan | from Lebesgue |
The same rigorous criteria that Cauchy had adopted in the Cours d'analyse are followed in presenting the fundamental concepts of calculus in the second of treaties he wrote for students of his courses, the Résumé des lešons données Ó l'École Royale Polytechnique. The last lectures of the course (XXI to XL) are devoted to integration.
"In integral calculus" - he writes in the introduction - "I thought it necessary to demonstrate in general the existence of the integrals or primitive functions, before revealing their various properties. For that, it was first of all necessary to establish the notion of an integral taken between two given limits, or defined integral."
The integral is thus defined independently from the derivate, but then the
two operations are compared, with a point of view in a way more similar to the
ideas on the measure of figures that had developed with Cavalieri and his
followers, and that had been swept apart with the success of infinitesimal
calculus, when the aspect of integration as the inverse operation than
differentiation prevails.
In order to define the integral of a function ![]() continuous with
continuous with ![]() varying in the interval
varying in the interval ![]() he considers a partition
he considers a partition ![]() of the interval in the elements
of the interval in the elements ![]() ,
, ![]() , ...,
, ..., ![]() , and defines the sum relative
to
, and defines the sum relative
to ![]() , nowaday called "Cauchy's", as
, nowaday called "Cauchy's", as
![]() .
Having established that, he proves that, thickening the
partition, the intervals become "very small",
.
Having established that, he proves that, thickening the
partition, the intervals become "very small",
the value of
will end up being visibly constant, or in other words will end up reaching a certain limit that will only depend on the form of the function
and on the extreme values attributed to variable
. This limit is what is called a defined integral.
Cauchy's new idea still presents many incomplete or unsatisfactory
aspects, on which later discussions develop. For example, the lack of a clear
distinction between continuity and uniform continuity, which was later the
object of studies by Weierstrass and his school; the lack of a systematisation
of irrational numbers that makes the existence of a limit of sums ambiguous.
A
particularly serious shortcoming, especially in the treatment of Fourier series,
is that the definition is valid for continuous functions or functions with a
finite number of discontinuities.
In the last part of his 1829 memo on
Fourier series, Sur la convergence des séries trigonométriques, Dirichlet
raises the issue of the integrability of functions with an infinite number of
discontinuity points, claiming that the set of admissible discontinuities must
be such that, translated into modern terms, its closure has no internal points.
As evidence of his claim, he brings the famous example of the function bearing
his name, that is the function ![]() whose value is 1 if
whose value is 1 if ![]() is rational and 0 if
is
is rational and 0 if
is ![]() not rational,
claiming that it is a non-integrable function.
not rational,
claiming that it is a non-integrable function.
A new definition of integral
that extends the class of integrable functions to functions with an infinite
number of discontinuity points is given by Bernhard Riemann in his tenure
habilitation thesis titled Ueber die Darstellbarkeit einer Funktion durch
eine trigonometrische Reihe, which is dated 1854 but remains practically
unknown until 1867, when Dedekind publishes it.
Here Riemann introduces the
integral that bears his name, considering the sums approximating from above and
from below. He then considers the problem of characterising integrable
functions. The final results are basically the following:
The necessary and sufficient condition to the integrability of a limited function
is that for every
and
there exists a partition of the definition interval into a finite number of intervals, such that the sum of the lengths of those in which the oscillation of the function is above
is smaller than
.
The general nature of this condition is shown by constructing an example of
integrable function which satisfies it, and which has a dense set of
discontinuity points, in contrast with the condition that Dirichlet considered
necessary.
The publication of Riemann's memo spurred a series of studies which
brought about developments in various directions. On the one hand, a specification of
topological concepts and of the properties of the straight line, which lead
Cantor to the foundation of set theory, and on the other, the construction of a
theory of measure which led to Lebesgue's theory.
In the years that followed, a number of works appeared, dealing with the study of the discontinuity
set of integrable functions that involve the jumps or oscillations of the
function, sparse sets, negligible sets, sets of the first species (that is, with
an empty nth derivate); among which we find contributions by Hankel,
Vitali, Du Bois-Reymond, Smith, Volterra. An organic systemisation of these
first developments on Riemann's integral can be found in the Foundations for
a theory of real variable functions (1878).
Beside the topological
characterisations, the idea of a "measure" of sets slowly develops. Stolz and
Harnack for example define the "content" ("Inhalt") of a set as the lower
bound of the sum of the lengths of the intervals whose union excludes the
given set. Cantor, at the same time, considers it the lower bound of the
measures of the external envelopes.
A more articulate concept of content is
introduced by Peano in 1887's Geometric Applications of Integral
Calculus. Jordan, in the second edition of the Cours d'Analyse,
develops a similar but more general tractation of n-dimensional space, with the
use of pluri-intervals. One defines the outer measure of a set A
as the lower bound of the measures of the
pluri-intervals that contain A, and as inner measure of A
the upper bound of the measures of the
pluri-intervals contained in A.
A set will then be measurable (according to Peano and Jordan) if its
inner and outer measures coincide.
Peano-Jordan's measure, thus defined,
results as additive (that is the measure of the union of two measurable
disjointed sets coincides with the sum of their measures) but not numerably
additive.
Harnack had already raised the issue of whether the sum of the
measures of a numerable infinity of disjointed intervals whose union is the
interval (a, b) were equal
to b-a, believing he could
answer negatively.
The issue was taken up again from a different point of
view by Borel, who demonstrated the result that Harnack had believed false and
uses it as a starting point for an axiomatic definition of measure, nucleating
the properties that he considered essential:
Borel then indicates how to construct a class of sets, which
were later called "Borel sets", which are measurable in this sense. These are
the minimum class containing the intervals which is stable according to
difference and to measurable union.
Borel's theory represents a great step forward,
especially because of the numerable additivity which was to reveal itself as one
of the most productive properties. In Borel's work, it appears, however, as a
technical means for the study of other issues, and is treated in an incomplete
and almost marginal way.
Lebesgue first understood the importance
of the new ideas and reworked them in his theory, which finds a first complete
exposition in the thesis Intégrale, longueur, aire published in 1902 on
the "Annals of Mathematics", and which is posed in a definitive way in the
Lešons sur l'intégration et la recherche des fonctions primitives
published in 1904.
Regarding measure, he joins Borel's ideas with Peano's and
Jordan's, defining firstly the external measure of a set E
as the lower extreme of the measures of the open sets that
contain E; then, in
the case that E is
limited and therefore contained in an interval Q, he defines the
outer measure of E as the difference between the measure of Q and
the outer one of Q-E. A set
will be measurable if its inner and outer measures coincide. Lebesgue then
demonstrated that the difference of two measurable sets is measurable and that
the union of a numerable infinity of measurable sets is measurable, and
therefore finds again Borel's conditions b) and c).
Lebesgue's most important
contribution is, however, the application of these ideas to integration theory.
Lebesgue himself muses on
the difference between his definition of integral and Riemann's,
in his popular Sur le development de la
notion d'intégrale, also using the comparison between the way a disorganised
merchant counts coins, and the way another will order them according to size. In
essence, having a much more flexible measurement available allows one to have
approximations which are no longer construed through a partition into
sub-intervals of the definition interval of the function to integrate, but
through a partition of the definition set into more general subsets on the basis
of the values which the function assumes.
Measure is not used any more to
characterise the discontinuity of functions that were integrable according to
Riemann, but to enlarge the class of functions that can be integrated. Moreover,
the use of a numerably additive measure, as well as making a great number of
sets measurable, brings about similar properties for the integral. This then can
enjoy more efficient properties such as that of passage to the limit under the
sign of integral, one of the cornerstones of the theory and a very powerful
instrument in many applications.
go back to the top of the page
![]() Luis Augustin
Cauchy
Luis Augustin
Cauchy
Résumé des lešons données à l'école Royale Polytechnique
Let us suppose that,
being a continuous function on the variable
between two finite limits
and
, one denotes as
,
, ...,
some new values of
interposed between those limits, and that always increase or decrease from the first limit to the second. One can use these values to divide the difference
into the elements
,
,
, ...
, which will all have the same sign. Having posited that, let us imagine that we multiply each element by the value of
corresponding to the origin of the same element, that is the element
by
, the element
by
, and finally the element
by
; let
be the sum of products thus obtained. Quantity S will obviously depend: 1)on the number n of the elements into which the difference
will be divided; 2) on the values of these elements themselves, and, consequently, on the subdivision method adopted. Now it is important to remark that if the numerical values of elements become very small and the number n very big, the subdivision method will have an invisible influence on the value
[...]
go back to the top of the page
![]() Bernhard Riemann
Bernhard Riemann
▄ber die Darstellbarkeit einer Funktion durch eine trigonometrische
Reihe
The incertitude that reigns on some fundamental points of the theory of undefined integrals forces us to preface with some words on the concept of defined integral and on the scope of its validity. Then, first of all: what is meant by
? To establish that, let us take between a and b a series of values
,
, ...,
that follow each other, and let us denote for brevity
as
,
as
,...,
as
and as
a proper positive fraction. The value of the sum
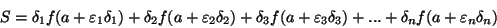
will then depend on the choice of intervalsand of
. If it has the property, no matter how chosen
and
, of infinitely approximating a prefixed limit A, as soon as they will become infinitely small, then this value is called
[...]
go back to the top of the page
![]() Giuseppe Peano
Giuseppe Peano
Applicazioni geometriche del calcolo integrale
The points of a straight line that are between two given points, considering or not considering those two points, form a field, which is called a rectilinear segment. Its length is a principal quantity: every field formed by a finite number of segments also has a length comparable to that of a given segment.
Let us take now a field formed by points on a straight line, no matter how given. We can, in general, imagine fields made of a finite number of segments, of which the given field is part, and we could imagine other fields also made of a finite number of segments, which are part of the given field. Each of these fields has a length, and the length of the former is greater than the length of the latter.
If the lower limit of the length of the first fields coincides with the upper limit of the lengths of the seconds, to this common value we will give the name of length of the given rectilinear field. But it could be that those limits are not equal, and therefore that the lower limit of the former lengths is greater than the upper limit of the latter. In this case we will say that the proposed field does not have a length comparable to that of a rectilinear segment, and to the lower limit of the former lengths we can give the name of external length of the given field, and call its internal length the upper limit of the latter.
![]() Camille Jordan
Camille Jordan
Cours d'analyse de L'école Polytechnique
36. We will then try to narrow the concept of extension of this object (which we can call in particular length, area, or volume, when the number of dimensions is 1, 2 or 3).
To fix down ideas, let us consider the case of two dimensions. Each point (u,v) of E can be geometrically represented on a plane of which u and v are the coordinates. Let us decompose this plane, with parallels to the axes, into squares with sides r. Among these, the set of the squares that are internal to E form a domain S internal to E; the set of those which are internal to E and that intersect its boundary form a new domain S+S' to which E is internal. These domains have a determined area that we will indicate, again, as S and S+S'.
Let us vary our decomposition into squares so that r tends to zero; areas S and S+S' will tend towards fixed limits [...].
go back to the top of the page
![]() Émile Borel
Émile Borel
Lešons sur la théorie des fonctions
Here are the new definitions: if a set E has as a measure s, and contains all the points of a set E' the measure of which is s', we can say that set E-E', formed by the points of E that do not belong to E', has the measure s-s'; moreover, if a set is the sum of a numerable infinity of sets with no parts in common, its measure will be the sum of the measures of its parts, and finally if the sets E and E' have, because of these definitions, measures s and s' and E includes all the points of E', the set E-E' will have the measure s-s'.
The fundamental theorem which we have demonstrated on page 41-43 assures us that these definitions will never be in contradiction with each other; we are therefore free to adopt them; we are also confident that the measure of a set can never be a negative quantity; but a set can have a measure zero and the power of the continuum. Thus is the set E considered below [...].
go back to the top of the page
![]() Henri Lebesgue
Henri Lebesgue
Intégrale, longueur, aire
3. Given a set
one can in an infinite variety of ways include its points in an interval or in a numerable infinity of intervals. The set
of the points of these intervals contains
, therefore measure
of
is at most equal to the one
of
, that is at most equal to the sum of the lengths of the intervals considered. The lower limit of this sum is an upper limit of
; we will call it the outer measure of
,
.
Let us suppose that all the points ofbelong to a segment
. We will call a complementary of
by
,
, the set
. Since the measure of
is at most
, the measure of
is at least
. This number does not depend on the segments containing
chosen; we will call it the inner measure of
,
[...].
We will call a measurable set that whose inner and outer measures are equal, the common value of these two numbers will be the measure of the set, if the issue of measure is possible. From the properties that follow it will result that the number
thus defined satisfies the conditions of the measurement problem if one only considers the measurable sets.
go back to the top of the page