Limiti delle distribuzioni binomiale e poissoniana

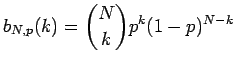
Il seguente codice permette di visualizzare il confronto fra la distribuzione binomiale

$$b_{N,p}(k) = \binom{N}{k} p^k (1-p)^{N-k}$$

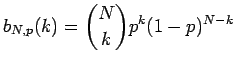
e il suo limite per $N\cdot p \ll N$, ovvero la distribuzione di Poisson con parametro $\lambda = Np$

$$p_{\lambda}(k) = \frac{\lambda^k}{k!}e^{-\lambda}$$

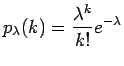
binpois <-function(n=10000,p=0.001) {
 lambda=n*p
 sd=sqrt(n*p*(1-p))
# scegliamo i limiti del plot come valore atteso 
# +/- 5 deviazioni standard 
 x=as.integer(lambda-5*sd):as.integer(lambda+5*sd)

 ybinom=dbinom(x,size=n,prob=p)
 ypois=dpois(x,lambda=lambda)

 plot(x,ybinom,type="s")
 points(x,ypois,type="s",col="red")
}

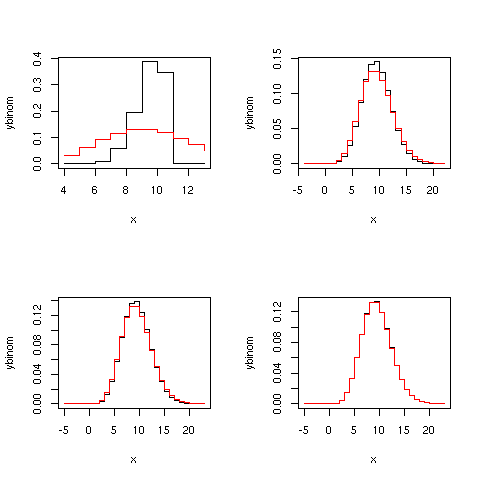
par(mfrow=c(2,2))
binpois(10,0.9)
binpois(50,0.18)
binpois(100,0.09) 
binpois(500,0.018)

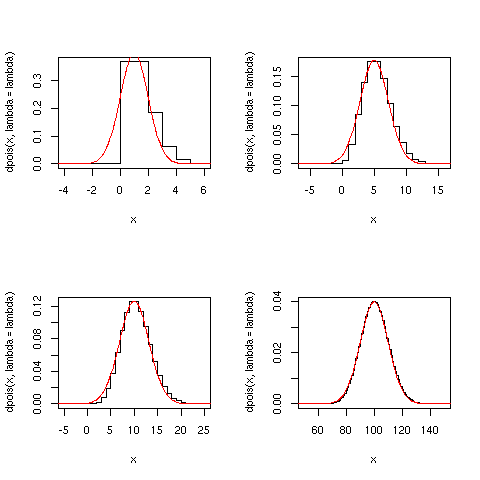
Analogamente possiamo confrontare la distribuzione di Poisson col suo limite asintotico, ovvero la gaussiana con valore atteso e varianza pari a $\lambda$:

gauspois <-function(lambda) {
 sd=sqrt(lambda)
 x=as.integer(lambda-5*sd):as.integer(lambda+5*sd)
 plot(x,dpois(x,lambda=lambda),type="s")
 curve(dnorm(x,mean=lambda,sd=sd),add=T,col="red")
}

par(mfrow=c(2,2))
gauspois(1)
gauspois(5) 
gauspois(10) 
gauspois(100)