"Gara Matematica" del 9 Aprile 2001
|
|
| (*) |
Se x > 68 allora basta risolvere: x - 68 = 2y e y = 2x, da cui x - 68 = 4x, che non fornisce soluzioni al nostro problema (x = -17 non è accettabile).
Se x < 68 allora troviamo x+32=2y e y-1=2x, da cui si ricavano x = 10 e y = 21.
Secondo metodo:
Dall'equazione (*) si ottiene: 98y = 199x + 68.
Essendo 199 un numero dispari, x dovrà essere pari e tale che 199x + 68 sia un multiplo di 98, oppure 199x/2 + 34 multiplo di 49. Quindi si ricava: x = 10, y = 21.
Poiché deve risultare x = a + b + c + m + n e poiché la somma di due numeri interi compresi tra 0 e 9999 è un numero compreso tra 0 e 19998 (= 2 * 9999) si ha che
Il Mago deve poter concludere con successo il numero di magia nell'eventualità che b e c siano entrambi zero. Pertanto dovrà essere
D'altra parte il mago deve poter fronteggiare la situazione anche nel caso in cui b e c siano entrambi 9999. Di conseguenza x deve soddisfare
da cui
Quindi la cosa giusta da fare per il Mago è scrivere sul foglio x = a + 19998 e scegliere m e n in modo che sia
Ciò è possibile sempre, ad esempio scegliendo m = 9999 - b e n = 9999 - c entrambi numeri interi compresi tra 0 e 9999.
La strategia, come segue dal ragionamento qui riportato, è unica. Un numero x > a + 19998 porta al fallimento del numero di magia se b = c = 0, mentre un numero x < a + 19998 farà fare una brutta figura al Mago qualora il pubblico scelga b = c = 9999.
e il rapporto cercato è quindi VP/VT=1/2.
Il poliedro P è un ottaedro (ricordiamo che un ottaedro è un solido platonico formato da 8 facce triangolari, 12 spigoli e 6 vertici) regolare di spigolo lungo x/2, infatti ognuno dei quattro tagli crea una faccia a forma di triangolo equilatero di lato x/2 e di ognuna delle quattro facce del tetraedro iniziale rimane solo un triangolo equilatero sempre di lato x/2. Siccome il diametro di un poliedro è la massima distanza tra due suoi vertici, avremo ovviamente diam(T)= x. Presi invece due vertici di P essi sono o adiacenti allo stesso spigolo e distano quindi x/2 oppure sono opposti ed in questo caso distano x
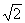 /2 in quanto si trovano ai due vertici
opposti di un quadrato i cui lati sono quattro spigoli dell'ottaedro. Dunque
/2 in quanto si trovano ai due vertici
opposti di un quadrato i cui lati sono quattro spigoli dell'ottaedro. Dunque
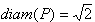 x/2 ed il rapporto richiesto è
diam(P)/diam(T) =
x/2 ed il rapporto richiesto è
diam(P)/diam(T) = 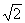 /2.
/2.Ricordiamo ora che una retta dello spazio si dice asse di simmetria di un solido se tale solido è invariante per rotazioni di 180 gradi attorno a tale retta (ovvero per simmetrie rispetto alla retta). Necessariamente l'asse di simmetria passa per il baricentro del solido, in quanto il solido originario ed il suo ruotato, essendo uguali, hanno lo stesso baricentro. Inoltre, se si considera un poliedro, una rotazione per cui il poliedro è invariante manda necessariamente vertici in vertici. Notiamo poi che le rotazioni di 180 gradi lasciano fissi i punti che si trovano sull'asse e scambiano a due a due gli altri punti dello spazio, dunque i vertici di un poliedro o rimangono fissi (se si trovano sull'asse di simmetria) oppure vengono scambiati a due a due.
Per quanto riguarda il tetraedro T, notiamo che se a è un asse di simmetria, allora necessariamente due vertici di T devono venire scambiati da tale simmetria (non è possibile che tutti i vertici di T stiano su una stessa retta). Necessariamente l'asse di simmetria passa dal punto medio del segmento individuato dai due vertici scambiati, e dal baricentro di T. Quindi passa anche dal punto medio dello spigolo opposto. Siccome gli spigoli in totale sono 6, le coppie di spigoli opposti sono 3 e dunque 3 sono gli assi di simmetria di T.
Supponiamo ora di avere un asse di simmetria per l'ottaedro P e siano V e W due vertici che vengono scambiati da tale simmetria. Se V e W sono adiacenti ad uno stesso spigolo s allora l'asse di simmetria deve passare dal punto medio di s, dal centro di P e quindi anche dal punto medio dello spigolo opposto ad s. Una retta siffatta è effettivamente un asse di simmetria per P e il numero di tali assi è pari al numero di coppie di spigoli opposti di P che è 12 / 2 = 6.
Se V e W non sono adiacenti allora sono opposti, e l'asse di simmetria si trova sul piano di simmetria del segmento VW ovvero sul piano contenente gli altri quattro vertici. Se due vertici adiacenti dei quattro rimasti vengono scambiati allora torniamo al caso precedente. Se invece vengono scambiati altri due vertici opposti allora l'asse deve passare per i due vertici opposti rimanenti. Siccome le coppie di vertici opposti sono 3, abbiamo trovato altri 3 assi di simmetria (che sono gli stessi trovati per il tetraedro, visto che i vertici di P si trovano sui punti medi degli spigoli di T). In totale dunque abbiamo 9 simmetrie.
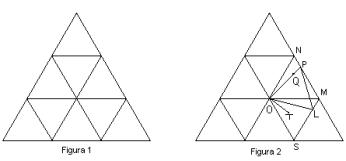
Figura 1
Comunque si scelgano dieci punti del triangolo, per il "principio dei cassetti", almeno due devono cadere in uno stesso triangolo dei nove in cui abbiamo suddiviso quello di partenza. Questi due punti distano l'uno dall'altro non più della massima distanza che si puù realizzare all'interno di un triangolino, ciò non più di 10 cm.
Anche scegliendo solo nove punti del triangolo possiamo affermare che ne esistono sempre due che distano al più 10 cm. Infatti, supponiamo per assurdo che esistano nove punti del triangolo che distano l'uno dall'altro più di 10 cm. Chiaramente ciascuno dei nove triangoli di lato 10 cm deve contenere uno e uno soltanto di questi nove punti. Consideriamo adesso soltanto i sei punti che stanno nei triangoli che non contengono i vertici del triangolo di partenza. Chiamiamo Q il punto che sta nel triangolo OMN e T il punto che sta nel triangolo OSM (figura 2): dimostriamo che l'angolo QOT è strettamente maggiore di 60 gradi.
Basta, a tale scopo, far vedere che T sta all'interno del triangolo OSL. Prolungando il segmento OQ fino ad incontrare in P il lato del triangolo e prendendo L sul lato MS in modo che l?angolo POL sia di 60 gradi, si costruisce il triangolo equilatero OLP, che ha lato minore di 10 cm. Osserviamo che il punto T non può appartenere al triangolo OLM in quanto, per costruzione, la sua distanza da Q sarebbe al più 10 cm. Pertanto T deve stare all'interno del triangolo OSL.
Il ragionamento fatto vale per ciascuno dei sei angoli con vertice in 0, determinati dalle coppie di punti che stanno in triangoli consecutivi. Si trova così che la somma di tali angoli è strettamente maggiore di 360 gradi: questo è assurdo, in quanto tale somma deve essere uguale all'angolo giro.