Testo della "Gara Matematica"
del 9 Aprile 2001
-
Francesco, rimasto senza soldi, va in banca per incassare un assegno in euro.
Il cassiere della banca inverte il numero di euro con quello dei centesimi di
euro. Francesco non si accorge di niente, ma dopo aver pagato al bar 68
centesimi di euro per un caffè si rende conto di avere in tasca
esattamente il doppio di quanto avrebbe dovuto incassare. A quanto ammontava
l'importo esatto dell'assegno?
-
Marco racconta ad Anna di aver letto su un libro il seguente "numero di magia".
Il "mago" di turno chiede ad uno spettatore di scrivere un numero di al
più quattro cifre (tra 0 e 9999, estremi inclusi) alla lavagna e quindi
ne scrive un altro (non necessariamente di quattro cifre) su un foglio, in modo
che nessuno lo veda. A questo punto il mago dice al pubblico che ha bisogno di
altri quattro numeri (di al più quattro cifre); due se li fa dare dal
pubblico e due li scrive lui stesso. Subito dopo aver scritto il quinto numero,
il mago somma i numeri alla lavagna e, nello stupore generale, mostra a tutti
che il risultato è proprio il numero che aveva scritto sul foglio in
precedenza.
Appena finito il racconto, Anna sorride ed aggiunge che c'è un'unica
strategia che il mago può e deve seguire. Sapreste dire quale?
Sapreste dimostrare che è unica?
-
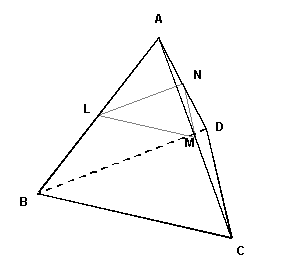
Un pezzo di sughero ha la forma di un tetraedro regolare T di vertici A, B, C
e D. Il sughero viene ridotto con quattro "tagli" nel modo seguente:
considerati i punti medi dei sei spigoli di T, il sughero è tagliato
lungo quattro piani determinati da tre punti medi (uno di questi tagli è
schematizzato in figura).
I vertici del tetraedro T vengono così eliminati uno alla volta.
Chiamiamo P il pezzetto di sughero rimasto.
Qual ? il rapporto tra il volume di P e quello di T ?
Qual ? il rapporto tra i loro diametri?
Quanti sono gli assi di simmetria di T e quanti quelli di P ?
-
Dato un triangolo equilatero di 30 cm di lato, dimostrare che comunque si
scelgano dieci punti del triangolo ne esistono sempre almeno due che distano
al più 10 cm.
Potremmo affermare la stessa cosa se scegliessimo solo nove punti del
triangolo?
|