Simulazioni MonteCarlo

Evoluzione di un prezzo

La variabile prezzo fra $n$ anni è data da

$$P(y+n) = P(y) \cdot r^n \cdot \prod_{i=1}^n(1+s_i)$$

La sua funzione densità è dunque ottenibile dalla convoluzione di Mellin di $n$ gaussiane, problema risolvibile tramite le funzioni di Bessel. Più semplicemente, possiamo risolvere il problema con una simulazione MonteCarlo:

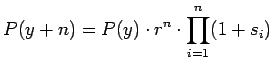
prezzo.corrente=1
rinfl= 1.02
spread=0.3
anno.corrente=2007 

prezzofuturo = function(anno) {
  n=anno-anno.corrente
  s = rnorm(n,sd=spread)
  prezzo.corrente * rinfl^n * prod(1+s)
}

simprezzo= function(anno,N=10000) {
 prezzi = c()
 for (i in 1:N) {
  prezzi[i] = prezzofuturo(anno)  
 }
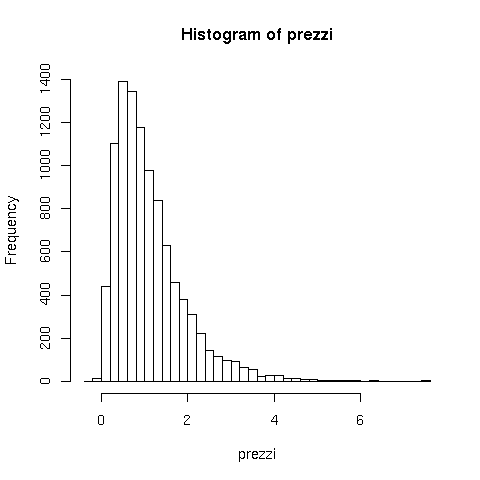
 hist(prezzi,breaks=50)
 cat("stima del valore atteso : ",mean(prezzi)," +/- ",sqrt(var(prezzi)/N)," \n");
 cat("stima della deviazione standard : ",sd(prezzi)," +/- ",
	sqrt((sum((prezzi-mean(prezzi))^4)/(N-1)-var(prezzi)^2)/N)," \n");
# calcoliamo la frazione oltre 3 e il suo errore 
 piuditre = length(prezzi[prezzi > 3])/N
 dpiuditre = sqrt(piuditre*(1-piuditre)/N)
 cat("frazione oltre 3 euro: ",piuditre," +/- ",dpiuditre," \n");
}

> simprezzo(2012)
stima del valore atteso :  1.113915  +/-  0.008181212  
stima della deviazione standard :  0.8181212  +/-  0.01719028  
frazione oltre 3 euro:  0.0335  +/-  0.001799382

Si noti che il valore atteso e la deviazione standard avrebbero potuto essere stimati usando la formula di propagazione degli errori:

$$E(P(y+n)) = P(y) \cdot r^n E(\prod_{i=1}^n(1+s_i)) = P(y) \cdot r^n \prod_{i=1}^n E(1+s_i) = P(y) \cdot r^n$$

$$\sigma((P(y+n)))/E(P(y+n)) \simeq \sqrt{\sum_{i=1}^n \left( \sigma(1+s_i)/E(1+s_i) \right)^2} = \sqrt{n} \sigma$$

Per $n=5$ otteniamo dunque $E(P(y+n))=1.104$, $\sigma((P(y+n)))=0.74$. L'approssimazione lineare usata nella propagazione degli errori ci avrebbe portato ad una sottostima della deviazione standard. In questa approssimazione, avremmo assunto la distribuzione di $P(Y+n)$ gaussiana e calcolato la probabilità di superare 3 euro come

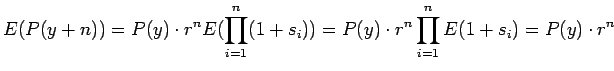
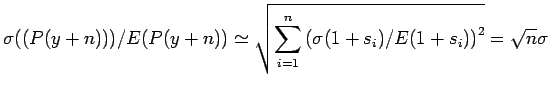
> atteso = prezzo.corrente * rinfl^5
> gsigma = atteso * spread * sqrt(5)
> 1 - pnorm((3-atteso)/gsigma) 
[1] 0.005236028

ottenendo $0.5 \%$ anzichè il valore corretto $(3.3 \pm 0.2) \%$ ottenuto dalla simulazione.

Metodo di Von Neumann

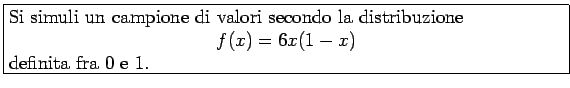
Scriviamo la funzione densità e il generatore random usando il metodo accept/reject di Von Neumann: generiamo coppie di punti $(X,Y)$ distribuite uniformemente negli intervalli $0<X<1$, $0<Y<max(f)=1.5$, e accettiamo solo i punti tali che $Y\leq f(X)$

dpol = function(x) {
ifelse(x<0 | x>1 , 0,6*x*(1-x) )
}

rpol = function(N) {
 out =c()
 for (i in 1:N) {
  y = runif(1,max=1.5)
  r = runif(1)
  while ( y > dpol(r) ) {
   y = runif(1,max=1.5)
   r = runif(1)
  }
  out[i]=r
 }
 out
}

# metodo alternativo (non garantisce la lunghezza del vettore prodotto):
rpol2 = function(N) {
 x=runif(N)
 y=runif(N,max=1.5)
 x[y <= dpol(x)]
}
 
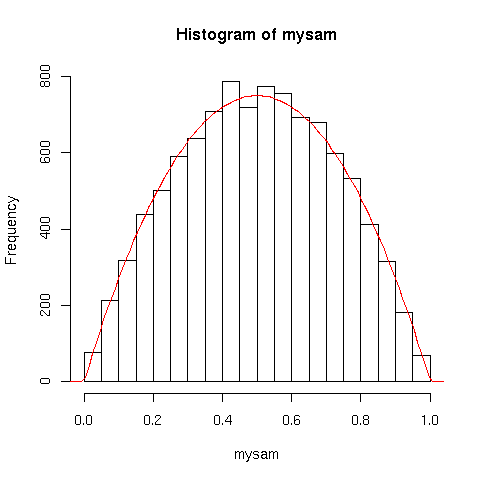
mysam=rpol(10000)
hist(mysam,breaks=seq(0,1,0.05))
curve(dpol(x)*0.05*10000,add=T,col="red")