Next: Test di Kolmogorov-Smirnov Up: Tests di ipotesi Previous: Tests di ipotesi

Subsections

Test di Pearson

Test di normalità tramite $\chi^2$

Abbiamo visto come in virtù del teorema del limite centrale la distribuzione densità della somma di

variabili distribuite uniformemente tenda rapidamente, al crescere di

, ad assomigliare a una distribuzione normale. Vogliamo ora rendere più quantitativo questo confronto, eseguendo un test $\chi^2$ per verificare l'ipotesi gaussiana su un campione di

valori simulati:

mychisqunif = function(n=3,N=1000) { sample = runif(N,-1,1) if (n >1) { for (i in 1:(n-1)) { sample = sample + runif(N,-1,1) } } sigmacentral=2*sqrt(n/12) delta=sigmacentral/20 h=hist(sample,breaks=seq(-1*n,1*n,delta)) curve(dnorm(x,sd=sigmacentral)*N*delta,add=T,col="red") x=h$mids dati=h$counts attesi = dnorm(x,sd=sigmacentral)*N*delta chi2 = sum((dati-attesi)^2/attesi) ngl = length(x) - 1 cat("chi2= ",chi2," dof=",ngl," p-value is ",1-pchisq(chi2,df=ngl),"\n") }

Con i valori , , il test dà tipicamente valori del p-value alti che non ci permettono di escludere l'ipotesi che il campione segua la distribuzione normale. Per poter ``accorgersi'' dai dati che la reale distribuzione non è una gaussiana, è necessario disporre di statistiche molto superiori:

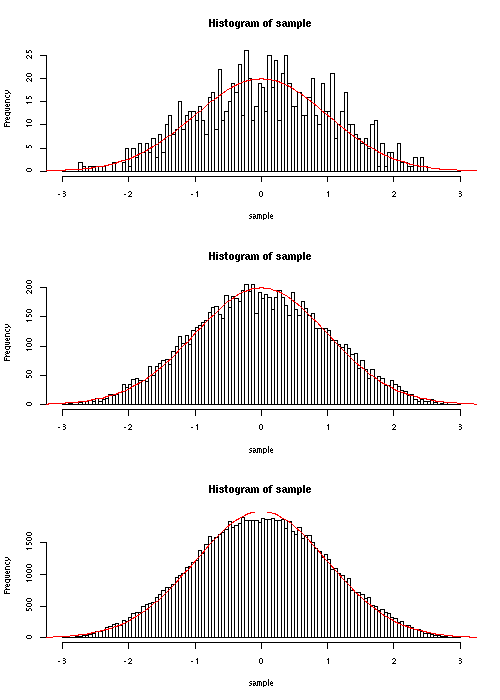
> par(mfrow=c(3,1)) > mychisqunif(3,1000) chi2= 138.0771 dof= 119 p-value is 0.1114694 > mychisqunif(3,10000) chi2= 157.4705 dof= 119 p-value is 0.01048201 > mychisqunif(3,100000) chi2= 703.2427 dof= 119 p-value is 0

Test di ipotesi poissoniana per conteggi di raggi cosmici

In un precedente esercizio abbiamo considerato i dati di un reale esperimento di conteggio di raggi cosmici, e verificato visivamente che il numero di eventi osservati in un intervallo di 2 minuti segue una ditribuzione di Poisson, come ci si attende nell'ipotesi di independenza degli eventi. Facciamo ora un confronto quantitativo per mezzo del test $\chi^2$ :

chisqcosmic = function() { df = read.table(file="CosmoData.txt",skip=7) c = df$V3 cm=mean(c) n=length(c) # costruiamo l'istogramma con bins di larghezza 1 centrati nei valori interi xmin=min(c)-1.5 xmax=max(c)+1.5 x=xmin:xmax h=hist(c,breaks=x) xp=h$mids dati=h$counts attesi = dpois(xp,lambda=cm)*n points(xp,attesi,type="p",col="red",pch=19) chi2 = sum((dati-attesi)^2/attesi) nbin=length(x) ngl = nbin - 2 cat("chi2= ",chi2," dof=",ngl," p-value is ",1-pchisq(chi2,df=ngl),"\n") }

Si noti che in questo caso il numero di gradi di libertà è N-2, poichè abbiamo usato i dati, oltre che per normalizzare la predizione, anche per stimarne il valore atteso.

Dal risultato p-value=65% concludiamo che i dati sono del tutto compatibili con l'ipotesi poissoniana.

Significatività di un debole segnale in presenza di fondo

$\framebox{\parbox{\linewidth}{ I valori nel file \\ /afs/math.unifi.it/service/... ...i che non vi sia nessun oggetto osservato con significatività $\alpha_S=5\%$. }}$

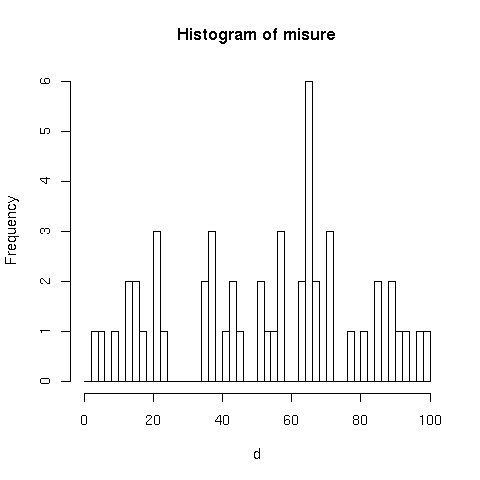
Contando la frequenza delle osservazioni in intervalli di 2 m, si osserva un possibile segnale intorno al valore $d\sim 65$ m :

misure = scan("/afs/math.unifi.it/service/Rdsets/ricercasegnale.rdata") h=hist(misure,breaks=seq(0,100,2))

Dai conteggi in istogramma possiamo calcolare il $\chi^2$ :

> dati=h$counts > ngl = length(dati) > fondo.atteso=1.04 # per bin > attesi=rep(fondo.atteso,ngl) > chi2 = sum((dati-attesi)^2/attesi) > cat("chi2= ",chi2," dof=",ngl," p-value is ",1-pchisq(chi2,df=ngl),"\n") chi2= 68.26923 dof= 50 p-value is 0.0438842

Essendo il p-value ottenuto inferiore ad $\alpha_S$ , potremmo concludere che i dati non sono compatibili con un fondo uniforme. Tuttavia, dato il basso valore dei conteggi, non possiamo aspettarci che la distribuzione di Pearson sia una buona approssimazione per la distribuzione del nostro $\chi^2$ . Nel caso di bassi ( $\lesssim 5$ ) conteggi, la distribuzione del $\chi^2$ dipende dal caso in esame, e per calcolare il valore corretto del p-value è necessario determinare la distribuzione corretta del $\chi^2$ simulando un gran numero di analoghi esperimenti nell'ipotesi nulla.

lowsignal = function(Nsim=5000) { misure = scan("/afs/math.unifi.it/service/Rdsets/ricercasegnale.rdata") h=hist(misure,breaks=seq(0,100,2)) dati=h$counts ngl = length(dati) fondo.atteso=1.04 # per bin attesi=rep(fondo.atteso,ngl) # simuliamo Nsim esperimenti con solo fondo e mettiamo nel vettore # simchi2 i valori del chi2 ottenuto in ciascun esperimento simchi2=c() for (i in 1:Nsim) { simset=rpois(ngl,lambda=fondo.atteso) simchi2[i]=sum((simset-attesi)^2/attesi) } # calcoliamo la frazione di esperimenti simulati con un valore di chi2 # superiore a quello osservato np=length(simchi2[simchi2>=chi2]) pv=np/Nsim dpv=sqrt(pv*(1-pv)/Nsim) cat("correct p-value is ",pv," +/- ",dpv,"\n") # confrontiamo la distribuzione di chi2 simulata # con quella di Pearson ch=hist(simchi2,breaks=50) delta=ch$breaks[2]-ch$breaks[1] curve(dchisq(x,df=ngl)*Nsim*delta,add=T,col="red") } > lowsignal() correct p-value is 0.0852 +/- 0.003948188

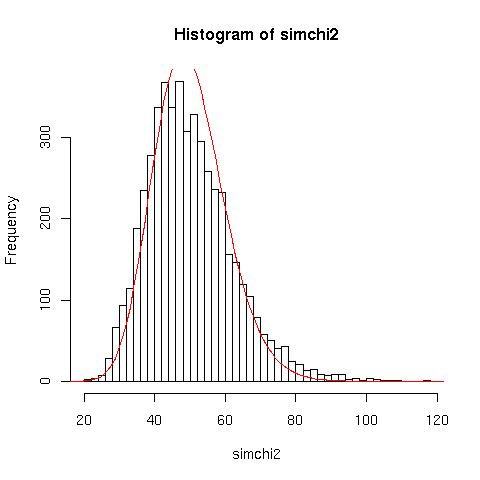
Notiamo che la reale distribuzione del $\chi^2$ ha code più importanti rispetto a quella attesa nel limite asintotico di grandi conteggi, per cui il valore corretto del p-value è sensibilmente maggiore di quanto stimato in precedenza.

Concludiamo dunque che entro il limite di significatività dato, i dati sono compatibili con un fondo uniforme.

Next: Test di Kolmogorov-Smirnov Up: Tests di ipotesi Previous: Tests di ipotesi

2008-05-30