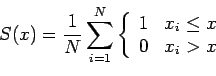

Confrontiamo innanzi tutto la funzione di probabilità cumulativa empirica del campione
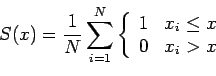
misure = scan("/afs/math.unifi.it/service/Rdsets/ricercasegnale.rdata")
plot.ecdf(misure)
curve(punif(x,min=0,max=100),add=T,col="red")
|
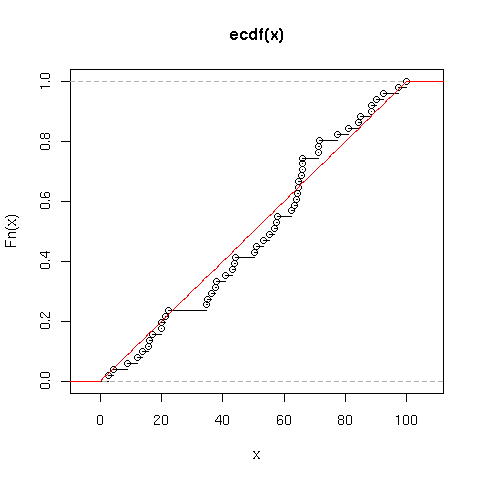
Il parametro ![]() del test, che è la massima distanza fra le due curve
nel grafico, e il corrispondente p-value sono ottenibili dalla
funzione ks.test:
del test, che è la massima distanza fra le due curve
nel grafico, e il corrispondente p-value sono ottenibili dalla
funzione ks.test:
> ks.test(misure,punif,min=0,max=100)
One-sample Kolmogorov-Smirnov test
data: misure
D = 0.112, p-value = 0.5084
alternative hypothesis: two.sided
|
I dati sono dunque compatibili con l'ipotesi nulla.