Discriminante di Fisher

Il classico problema di classificazione dell' iris

da un controllo visuale delle 4 variabili risulta evidente che la specie ``setosa'' può essere isolata dalle altre con un semplice taglio sulla variabile Petal.Length

library(MASS)
ldahist(iris$Petal.Length, iris$Species)

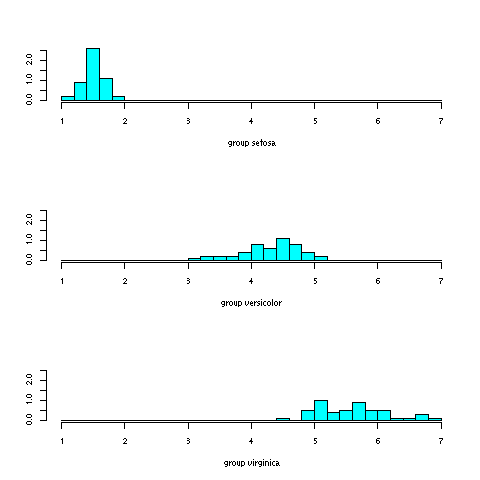
Costruiamo dunque un discriminante lineare per separare l'ipotesi ``versicolor'' dall'ipotesi alternativa ``virginica'':

myiris=iris[iris$Petal.Length>2.5,]
set.seed(99)
samp=sample(1:100,50)
myiris.train=myiris[samp,]
myiris.test =myiris[-samp,]

# calcolo delle medie nelle due ipotesi
mu0 = mean(myiris.train[myiris.train$Species=="versicolor",1:4])
mu1 = mean(myiris.train[myiris.train$Species=="virginica",1:4])

#calcolo delle matirice var/cov nelle due ipotesi
v0 = var(myiris.train[myiris.train$Species=="versicolor",1:4])
v1 = var(myiris.train[myiris.train$Species=="virginica",1:4])

#calcolo dei coefficienti lineari
a = solve(v0+v1) %*% (mu0-mu1)
print(a)

(si noti l'uso della funzione sample per estrarre casualmente 50 righe dal dataframe, e della funzione set.seed per poter riprodurre la stessa sequenza pseudorandom nel caso di ripetuta esecuzione del codice)

Possiamo a questo punto calcolare la funzione discriminante e osservare la separazione ottenuta sul campione di test:

discr = as.matrix(myiris.test[1:4]) %*% a
myiris.test = data.frame(myiris.test,fisher=discr)
ldahist(myiris.test$fisher,myiris.test$Species)

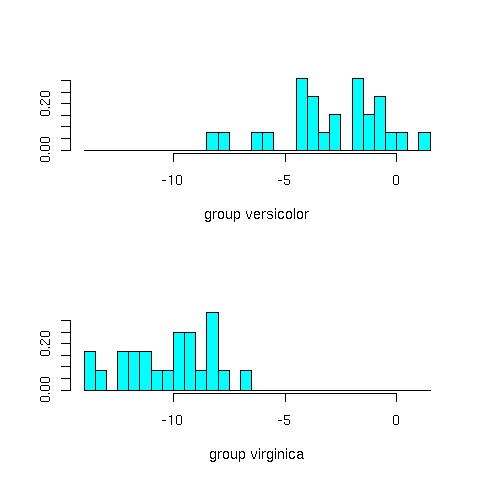
Il discriminante può essere ottenuto in modo equivalente con la funzione di R lda:

iris.lda2=lda(Species ~ . , myiris.train,prior=c(0,1,1)/2)
print(iris.lda2$scaling)

(i coefficienti ottenuti differiscono dal vettore $a$ ottenuto in precedenza di un arbitrario fattore di scala).

La funzione lda permette anche l'analisi nel caso di più ipotesi alternative, possiamo dunque usarla direttamente per separare le tre specie:

set.seed(99)
samp=sample(1:150,75)
myiris3.tr=iris[samp,]
myiris3.test=iris[-samp,]
iris.lda3=lda(Species ~ . , myiris3.tr, prior=c(1,1,1)/3)
print(iris.lda3$scaling)

Si ottengono in questo caso due statistiche discriminanti; dalla differenza degli autovalori ( $iris.lda3\$svd$) possiamo aspettarci che solo il primo sia significativo, come possiamo verificare graficamente:

a1= iris.lda3$scaling[,1]
a2= iris.lda3$scaling[,2]
myiris3.test = data.frame(myiris3.test,	fisher1= as.matrix(myiris3.test[1:4]) %*% a1,
                          fisher2= as.matrix(myiris3.test[1:4]) %*% a2 )
 
ldahist(myiris3.test$fisher1,myiris3.test$Species)
ldahist(myiris3.test$fisher2,myiris3.test$Species)