Rapporto di likelihood

Un esempio di controllo qualità

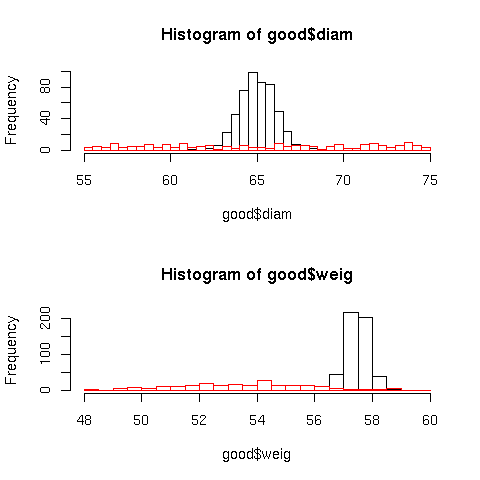
Utilizzando il campione di training, stimiamo i parametri incogniti (e relativi errori) delle distribuzioni per i due campioni ``good'' e ``bad'', che possono essere ricavati semplicemente dalle medie e i momenti delle distribuzioni:

tb=read.table('/afs/math.unifi.it/service/Rdsets/tennisballs.rdata')
good=subset(tb,clas=='OK',c(diam,weig))
bad=subset(tb,clas=='BAD',c(diam,weig))
par(mfrow=c(2,1))
hist(good$diam,breaks=seq(55,75,0.5))
hist(bad$diam,breaks=seq(55,75,0.5),add=T,border="red")
hist(good$weig,breaks=seq(48,60,0.5))
hist(bad$weig,breaks=seq(48,60,0.5),add=T,border="red")
par(mfrow=c(1,1))

ng=length(good$diam)
nb=length(bad$diam)
mu4d.good=sum((good$diam-mean(good$diam))^4)/ng
mu4w.good=sum((good$weig-mean(good$weig))^4)/ng
mu4w.bad=sum((bad$weig-mean(bad$weig))^4)/nb

sigma.diam.good = sd(good$diam)
dsigma.diam.good = 1/(2*sigma.diam.good)*sqrt((mu4d.good-var(good$diam)^2)/ng)
sigma.weig.good = sd(good$weig)
dsigma.weig.good = 1/(2*sigma.weig.good)*sqrt((mu4w.good-var(good$weig)^2)/ng)
mean.weig.bad = mean(bad$weig)
dmean.weig.bad = sd(bad$weig)/sqrt(nb)
sigma.weig.bad = sd(bad$weig)
dsigma.weig.bad = 1/(2*sigma.weig.bad)*sqrt((mu4w.bad-var(bad$weig)^2)/nb)

La migliore separazione dei due campioni è ottenuta con un taglio sul rapporto di likelihood

tennis.likratio= function(d,w) {
 (dnorm(d,mean=65.0,sd=sigma.diam.good)*dnorm(w,mean=57.5,sd=sigma.weig.good)) /
 (dunif(d,min=55,max=75) * dnorm(w,mean=mean.weig.bad,sd=sigma.weig.bad) )
}

ad esempio il criterio di qualità può essere definito come
$log(tennis.likratio(d,w)) > 0$

Per valutare la purezza delle palline prodotte, è necessario stimare le probabilità di errore di primo e secondo grado $\alpha$ e $\beta$:

$$p = \frac{N_{good}}{N_{good}+N_{bad}} = \frac{(1-\alpha)}{ (1-\alpha) + \beta N_{bad}/N_{good}}$$

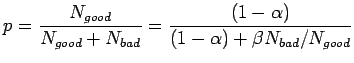
Queste possono essere valutate su un secondo campione di training, poichè la stima sul campione usato per valutare i parametri è necessariamente distorta. Assumendo la correttezza del modello, possiamo ottenere $\alpha$ e $\beta$ anche da una simulazione:

tennis.sim = function(Nsim=50000, dd.ok=sigma.diam.good, dw.ok= sigma.weig.good,
                      w.bad =mean.weig.bad, dw.bad=sigma.weig.bad ) {
 
 cut=0
 llik.good = log(tennis.likratio(rnorm(Nsim,mean=65.0,sd=dd.ok),rnorm(Nsim,mean=57.5,sd=dw.ok)))
 llik.bad =  log(tennis.likratio(runif(Nsim,min=55,max=75),rnorm(Nsim,mean=w.bad,sd=dw.bad)))
 alpha = length( llik.good[llik.good < cut])/Nsim
 cat("alpha=",alpha," +/- ",sqrt(alpha*(1-alpha)/Nsim),"\n")
 beta  = length( llik.bad[llik.bad > cut])/Nsim
 cat("beta=",beta," +/- ",sqrt(beta*(1-beta)/Nsim),"\n")
}

da cui otteniamo:

alpha= 0.00398  +/-  0.0002815727 
beta = 0.02068  +/-  0.0006364328

dove l'errore è solo quello dovuto alla statistica della simulazione e non abbiamo ancora considerato l'errore dovuto ai parametri delle distribuzioni. Per calcolare quest'ultimo, dovremmo valutare tramite simulazione la dipendenza di $\alpha$ e $\beta$ dai parametri e propagare gli errori. Per avere più rapidamente un ragionevole limite inferiore per la purezza, è tuttavia sufficiente una stima pessimistica di $\alpha$ e $\beta$ ottenuta alterando tutti i parametri di una deviazione standard in senso ``peggiorativo'':

> tennis.sim(Nsim=50000, dd.ok=sigma.diam.good+dsigma.diam.good,
                       dw.ok= sigma.weig.good + dsigma.weig.good,
                       w.bad =mean.weig.bad + dmean.weig.bad , 
                       dw.bad= sigma.weig.bad + dsigma.weig.bad)
alpha= 0.00522  +/-  0.0003222655 
beta = 0.02506  +/-  0.0006990278

Otteniamo dunque

$$p > \frac{(1-0.0052)}{(1-0.0052)+ 0.025  \cdot  0.0427} = 0.9989$$

dove il rapporto $N_{bad}/N_{good}$ è stato stimato da

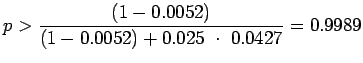
> prod=tb[is.na(tb$clas),]
> llprod=log(tennis.likratio(prod$diam,prod$weig))
> length(llprod[llprod<0])/length(llprod[llprod>0])
[1] 0.04273877