Next: Minimi quadrati: Modelli lineari Up: Fits parametrici Previous: Fits parametrici

Subsections

Minimi quadrati: Modelli lineari

Caduta dei gravi

$\framebox{\parbox{\linewidth}{ La tabella nel file \\ /afs/math.unifi.it/servic... ... e costanti sulle misure di $h$ ed errori trascurabili sulle misure di $t$. }}$

I dati possono essere descritti dal modello lineare

$\displaystyle h= h_0 - g t^2/2 +\epsilon$

dove $\epsilon$ rappresenta l'errore casuale che segue una distribuzione gaussiana con $\sigma$ ignota. La soluzione di massima verosimiglianza è ottenuta dall'analisi di regressione minimizzando i minimi quadrati in funzione dei parametri incogniti

par(mfrow=c(2,1)) cg=read.table("/afs/math.unifi.it/service/Rdsets/cadutalibera.rdata") attach(cg) plot(altezza ~ tempo) n=length(altezza) # creiamo la matrice del modello A= matrix( nrow=n,ncol=2,data=c(rep(1,n),-tempo^2/2)) K = solve(t(A) %*% A) # ricaviamo il vettore theta con la stima dei parametri h0 e g theta = K %*% t(A) %*% altezza # disegniamo la funzione ottenuta dal fit curve(theta[1]-theta[2]*x^2/2,add=T,col="blue") # stima dell'errore su h residui = altezza - A %*% theta plot(residui) var.h = sum(residui^2)/(n-2) cat("errore stimato su h:",sqrt(var.h),"\n") # stima dell'errore sui parametri V.theta = var.h * K sigma.theta = sqrt(diag(V.theta)) cat("h0=",theta[1]," +/- ",sigma.theta[1],"\n") cat("g=",theta[2]," +/- ",sigma.theta[2],"\n") # h0= 2.097576 +/- 0.01057463 # g= 10.24337 +/- 0.3232533

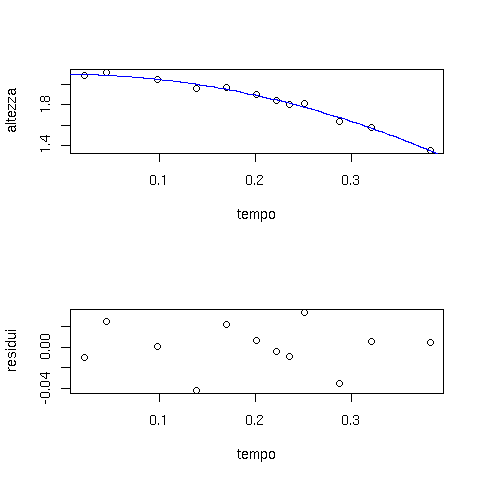
Il grafico che mostra i residui in funzione di ci permette di verificare l'assenza di una eventuale dipendenza residua non inclusa nel modello.

la funzione lm() di R ci permette di svolgere il calcolo con un'unica chiamata:

> summary(lm(altezza ~ I(-tempo^2/2),data=cg)) Call: lm(formula = altezza ~ I(-tempo^2/2), data = cg) Residuals: Min 1Q Median 3Q Max -0.041615 -0.009098 0.003080 0.010776 0.033711 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.09758 0.01057 198.36 < 2e-16 *** I(-tempo^2/2) 10.24337 0.32325 31.69 2.30e-11 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.02358 on 10 degrees of freedom Multiple R-Squared: 0.9901, Adjusted R-squared: 0.9892 F-statistic: 1004 on 1 and 10 DF, p-value: 2.303e-11

(si noti che nella formula che descrive il modello l'intercetta è implicita; se non avessimo voluto includerla avremmo scritto

lm(altezza ~ 0 + I(tempo^2))

)

Test $\chi^2$ sul fit

$\framebox{\parbox{\linewidth}{ Si esegua un test della bontà del fit dell'eserci... ...do che lo strumento con cui si misurano le altezze ha una risoluzione di 3 cm }}$

Conscendo $\sigma_h = 0.03$ m, possiamo ora calcolare il $\chi^2$ del fit e il corrispondente p-value:

sigma.y = 0.03 chi2 = sum(residui^2)/sigma.y^2 cat("chi2=",chi2," con ",n-2," gradi di liberta'\n" ) cat("p-value = ",1-pchisq(chi2,df=n-2),"\n")

Il valore ottenuto p-value=0.80 ci conferma la validità del modello.

Gli errori su possono essere specificati nella funzione lm() di R tramite l'argomento che rappresenta il vettore dei pesi $1/\sigma_h^2$ :

fit = lm(altezza ~ I(tempo^2/2), weights=rep(1/sigma.y^2,n)) chi2 = deviance(fit)

Intervallo di confidenza sulla predizione del fit

$\framebox{\parbox{\linewidth}{ Si stimi il valore atteso di $h$ al tempo $t'=0.6$ s e il corrispondente intervallo di confidenza con livello $\alpha$=0.95\%. }}$

La stima di è ovviamente

$\displaystyle \bar{h}(t') = \bar{h_0} - \bar{g} t'^2/2 = A(t') \theta$

dove

è la matrice del modello calcolata nel punto

e $\theta$ il vettore

La stima della sua varianza è ottenuta dalla formula di propagazione degli errori, che vale esattamente nel caso lineare:

$\displaystyle \bar{\sigma}^2(\bar{h}(t')) = \bar{\sigma}^2(h_0) + (t'^2/2)^2 \bar{\sigma}^2(g) +2 (-t'^2/2) \overline{cov}(h_0,g) = A(t') V_{\theta} A^T(t')$

(L'espressione matriciale ci permette di estendere le formule al caso in cui

è un vettore di valori, nel qual caso l'ultima l'espressione diventa la matrice varianza/covarianza delle predizioni $\bar{h}(t')$ ).

La variabile

$\displaystyle t(h(t')) = (\bar{h}(t') - E(h(t')) )/\bar{\sigma}(\bar{h}(t'))$

segue una distribuzione di Student con

gradi di libertà. L'intervallo di confidenza è dunque ottenuto come segue:

mypred = function(tprime=0.6,alpha=0.95) { A.tprime= matrix( nrow=1,ncol=2,data=c( 1,-tprime^2/2)) h.pred= A.tprime %*% theta sigma.pred = sqrt(A.tprime %*% V.theta %*% t(A.tprime)) Nsigma = qt((1+alpha)/2,df=n-2) cat("h(",tprime,")=",h.pred, " +/- ",Nsigma*sigma.pred," C.L.=",alpha,"\n") } > mypred(0.6,0.95) h( 0.6 )= 0.2537696 +/- 0.1126419 C.L.= 0.95

Al solito, R prevede una funzione () per fare questo calcolo in una sola chiamata:

> myfit = lm(altezza ~ I(-tempo^2/2),data=cg) > predict(myfit,newdata=(tempo=0.6),interval="confidence",level=0.95) fit lwr upr [1,] 0.2537696 0.1411276 0.3664115

Fit di un istogramma: metodo iterativo

$\framebox{\parbox{\linewidth}{ Si esegua un fit delle misure di energia (in GeV)... ...che $\mu=5.2 $ GeV, $\sigma=0.3$ GeV, e si esegua un test di bontà del fit. }}$

In questo caso ci aspettiamo che i conteggi misurati in ogni intervallo seguano una distribuzione di Poisson con valore atteso . Possiamo dunque dare una prima stima della varianza $\sigma^2(k_i) = k_i$ e ottenere un primo fit minimizzando

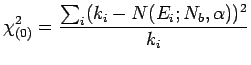
$\displaystyle \chi^2_{(0)} = \frac{\sum_i (k_i - N(E_i;N_b,\alpha))^2}{k_i}$

Assumendo la correttezza del modello, i valori dei conteggi ottenuti dal fit saranno una miglior stima di $\sigma^2(k_i)$ . Procediamo dunque in modo iterativo, fino ad ottenere una convergenza del valore di $\chi^2$ :

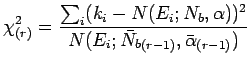
$\displaystyle \chi^2_{(r)} = \frac{\sum_i (k_i - N(E_i;N_b,\alpha))^2}{N(E_i;\bar{N_b}_{(r-1)},\bar{\alpha}_{(r-1)})}$

histofit = function() { sam=scan("/afs/math.unifi.it/service/Rdsets/gaussconfondo.rdata") iter=0 while (iter<5 ) { h=hist(sam,breaks=seq(0,10,0.2)) mu=5.2 sigma=0.3 x=h$mids k=h$counts n=length(k) if (iter == 0) { cat("######### Primo fit #########\n") dk2=k } else { dk2=A %*% theta cat("######### Iterazione ",iter," #########\n") } # costruiamo la matrice del modello e la matrice var/cov delle k A = matrix(ncol=2,nrow=N,data= c(rep(1,N) , exp(-(x-mu)^2/(2*sigma^2)))) V.k = matrix(ncol=N,nrow=N,data=0) diag(V.k) = dk2 V.theta = solve(t(A) %*% solve(V.k) %*% A ) theta = V.theta %*% t(A) %*% solve(V.k) %*% k cat("theta=",theta,"\n") cat(" +/- ",sqrt(diag(V.theta)),"\n") curve( theta[1] + theta[2] *exp(-(x-mu)^2/(2*sigma^2)),0,10,add=T,col="red" ) residui = k - A %*% theta chisq = sum(residui^2/dk2 ) cat ("chi2=",chisq," con ",N-2," g.d.l. p-value=",1-pchisq(chisq,df=N-2),"\n") iter=iter+1 } > histofit() ######### Primo fit ######### theta= 16.91985 156.4992 +/- 0.6252381 7.135217 chi2= 77.57949 con 48 g.d.l. p-value= 0.004377989 ######### Iterazione 1 ######### theta= 18.59739 154.8243 +/- 0.6275628 7.171216 chi2= 63.74022 con 48 g.d.l. p-value= 0.06366115 ######### Iterazione 2 ######### theta= 18.60706 154.6957 +/- 0.6573149 7.197776 chi2= 58.38637 con 48 g.d.l. p-value= 0.1448092 ######### Iterazione 3 ######### theta= 18.60719 154.6940 +/- 0.6574779 7.195656 ######### Iterazione 4 ######### theta= 18.60719 154.694 +/- 0.65748 7.195629 chi2= 58.36089 con 48 g.d.l. p-value= 0.1453295

Regressione lineare ``esplorativa'' nel caso multivariato

$\framebox{\parbox{\linewidth}{ Usando i dati nel dataframe $UScrime$ (pacchetto... ...nza $Ineq$, tenendo conto o meno della variabile prodotto interno lordo $GDP$ }}$

Il grafico

attach(MASS) plot(y ~ Ineq, data=UScrime)

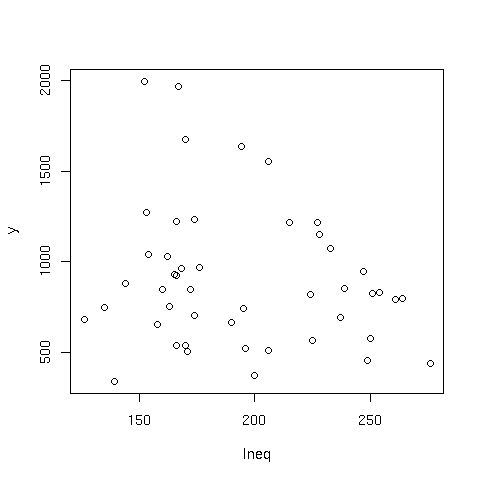
non mostra una evidente correlazione fra le due variabili, anche se suggerisce una possibile anticorrelazione. Esploriamo dunque il modello lineare
$y=y_0 + \theta \cdot Ineq + \epsilon$

> summary(lm(y ~ Ineq, data=UScrime)) Call: lm(formula = y ~ Ineq, data = UScrime) Residuals: Min 1Q Median 3Q Max -658.54 -271.38 -30.02 183.75 1017.06 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1241.773 281.478 4.412 6.33e-05 *** Ineq -1.736 1.422 -1.221 0.229

Otteniamo effettivamente un valore negativo per $\theta$ , tuttavia il test di Student dell'ipotesi $\theta=0$ dà p-value = 23 %, e non possiamo dunque affermare di aver messo in evidenza una dipendenza fra le due variabili.

Se ora consideriamo la variabile , notiamo che questa è evidentemente correlata con le altre due variabili:

# valutiamo i coefficienti di correlazione lineare > cor(UScrime[,c("y","Ineq","GDP")]) y Ineq GDP y 1.0000000 -0.1790237 0.4413199 Ineq -0.1790237 1.0000000 -0.8839973 GDP 0.4413199 -0.8839973 1.0000000 # e il loro errore: > sqrt( (1-cor(UScrime[,c("y","Ineq","GDP")])^2) / length(UScrime$y)) y Ineq GDP y 0.0000000 0.14350851 0.13089192 Ineq 0.1435085 0.00000000 0.06819072 GDP 0.1308919 0.06819072 0.00000000

Verifichiamo allora una possibile dipendenza di da dopo aver tenuto conto della dipendenza da con una semplice ipotesi lineare:
$y=y_0 + \theta_1 \cdot Ineq + \theta_2 \cdot GDP + \epsilon$

> summary(fit <- lm(y ~ Ineq + GDP, data=UScrime)) Call: lm(formula = y ~ Ineq + GDP, data = UScrime) Residuals: Min 1Q Median 3Q Max -610.09 -193.09 -16.01 108.05 814.69 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -3639.047 968.692 -3.757 0.000503 *** Ineq 9.364 2.424 3.863 0.000364 *** GDP 5.192 1.002 5.179 5.32e-06 ***

Vista la forte correlazione fra e , ci aspettiamo che i due parametri $\theta_1$ e $\theta_2$ siano pure correlati:

> cov2cor(vcov(fit)) (Intercept) Ineq GDP (Intercept) 1.0000000 -0.9660638 -0.9728075 Ineq -0.9660638 1.0000000 0.8839973 GDP -0.9728075 0.8839973 1.0000000

Essendo comunque i due parametri significativamente diversi da 0, possiamo concludere di aver messo in evidenza una correlazione positiva fra e per stati con lo stesso prodotto interno lordo. Possiamo visualizzare il risultato disegnando l'intervallo di confidenza per $\theta_1$ e $\theta_2$ , che nell'ipotesi di errori gaussiani è definito dai punti all'interno dell'ellisse di covarianza per cui

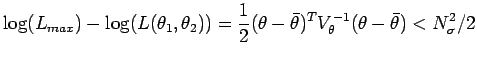
$\displaystyle \log(L_{max}) - \log(L(\theta_1,\theta_2)) = \frac{1}{2}(\theta - \bar{\theta})^T V_{\theta}^{-1} (\theta -\bar{\theta}) < N_{\sigma}^2/2$

dove

è la funzione di likelyhood e $\theta$ è il vettore ( $\theta_1$ , $\theta_2$ ).

il seguente codice disegna le ellissi corrispondenti a $N_{\sigma}=1,2,3$ , che nel caso bidimensionale corrisponde agli intervalli di confidenza 39.3 %, 86.5 %, 98.9 %

mylik = function(t1,t2,theta1,theta2,s1,s2,rho) { -1/(2*(1-rho)) * ( (t1-theta1)^2/s1^2 + (t2-theta2)^2/s2^2 - 2*rho* (t1-theta1)/s1 *(t2-theta2)/s2) } nsigma=c(1,2,3) theta1=coef(fit)["Ineq"] theta2=coef(fit)["GDP"] s1=sqrt(vcov(fit)["Ineq","Ineq"]) s2= sqrt(vcov(fit)["GDP","GDP"]) rho = cov2cor(vcov(fit))["Ineq","GDP"] x=seq(-2,15,.1) y=seq(-2,15,.1) contour(x,y, outer(x,y,mylik, theta1=theta1, theta2=theta2,s1=s1,s2=s2,rho=rho), levels = -nsigma^2/2 , xlab=expression(theta[1]),ylab=expression(theta[2]))

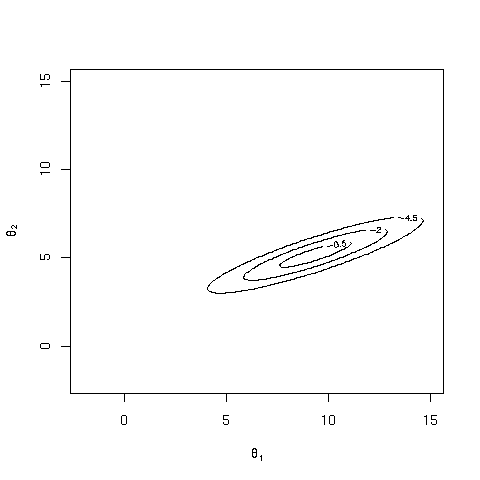
I residui parziali
$r_{Ineq} = y - ( y_0 + \theta_2 \cdot GDP )$
$r_{GDP} = y - ( y_0 + \theta_1 \cdot Ineq )$
permettono di visualizzare la dipendenza residua da ogni singola variabile dopo aver tenuto conto delle altre variabili del fit. Possono essere visualizzati tramite la funzione di R

termplot(fit,partial=T,se=T)

Sottolineiamo infine il fatto che i risultati di queste analisi di regressione possono mettere in evidenza le mutue dipendenze fra le variabili, ma non potranno mai dimostrare un rapporto di causa-effetto! Il modello deterministico delle dipendenze è lasciato all'interpretazione dell'analista...

Analisi della covarianza

$\framebox{\parbox{\linewidth}{ Usando i dati nel dataframe $Rubber$ (pacchetto ... ...llo migliora significativamente la stima dei valori attesi $loss(hard,tens)$. }}$

Testiamo l'ipotesi nulla tramite un'analisi della covarianza del modello M1. Estendiamo cioè l'idea dell'analisi della varianza al caso in cui la dispersione della variabile studiata può dipendere da una o più variabili continue tramite parametri:

$\displaystyle Q = \sum_i (y_i - \bar{y})^2 = \sum_i (y_i - \lambda_i)^2 + \sum_i (\lambda_i - \bar{y})^2 = Q_w + Q_b$

dove $\lambda_i$ sono i valori ottenuti dal fit lineare variando gli

parametri.
Nell'ipotesi nulla, la variabile

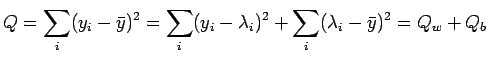
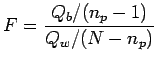
$\displaystyle F = \frac{Q_b/(n_p-1)}{Q_w/(N-n_p)}$

segue una distribuzione di Fisher con

gradi di libertà.

library(MASS) fit1=lm(loss~hard + tens,data=Rubber) np=3 N=length(Rubber$loss) Qb=sum((fit1$fitted.values-mean(Rubber$loss))^2) Qw=deviance(fit1) F = Qb/(np-1) / ( Qw/(N-np) ) cat("F= ",F," p-value=",1-pf(F,df1=np-1,df2=N-np),"\n")

Il valore del p-value= $1.8\cdot10^{-11}$ dimostra la dipendenza fra le variabili, escludendo l'ipotesi nulla.
Si noti che il risultato di questa analisi è riportato anche dalla chiamata .
Si noti anche che nel caso di un singolo parametro di dipendenza (retta dei minimi quadrati),

$\displaystyle y = \theta_0 + \theta_1 g(x) + \epsilon$

l'analisi della covarianza è equivalente al test di Student dell'ipotesi $\theta_1=0$ , con

, ad esempio nel caso

> summary(lm(loss~tens,data=Rubber)) Call: lm(formula = loss ~ tens, data = Rubber) Residuals: Min 1Q Median 3Q Max -155.640 -59.919 2.795 61.221 183.285 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 305.2248 79.9962 3.815 0.000688 *** tens -0.7192 0.4347 -1.654 0.109232 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 85.56 on 28 degrees of freedom Multiple R-Squared: 0.08904, Adjusted R-squared: 0.0565 F-statistic: 2.737 on 1 and 28 DF, p-value: 0.1092

si ha e il p-value di entrambi i tests è pari a .

Per il confronto fra i modelli M1 e M5, possiamo usare ancora un'analisi di varianza scomponendo i residui del primo fit:

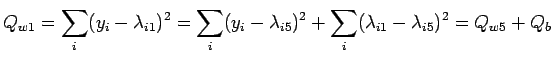
$\displaystyle Q_{w1} = \sum_i (y_i - \lambda_{i1})^2 = \sum_i (y_i - \lambda_{i5})^2 + \sum_i (\lambda_{i1} - \lambda_{i5})^2 = Q_{w5} + Q_b$

Se entrambi i modelli descrivessero correttamente i valori attesi di

, la quantità

sarebbe dovuta solamente a fluttuazioni casuali e la variabile

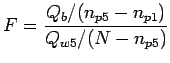
$\displaystyle F = \frac{Q_b/(n_{p5}-n_{p1})}{Q_{w5}/(N-n_{p5})}$

seguirebbe la distribuzione di Fisher con $n_{p5}-n_{p1},N-n_{p5}$ gradi di libertà.

library(MASS) N=length(Rubber$loss) fit1=lm(loss~hard + tens,data=Rubber) np1=3 fit5=lm(loss~hard + tens + I(tens^2) + I(tens^3)+ I(tens^4)+ I(tens^5),data=Rubber) np5=7 Qb=sum((resid(fit1)-resid(fit5))^2) Qw5=deviance(fit5) F = Qb/(np5-np1) / ( Qw5/(N-np5) ) cat("F= ",F," p-value=",1-pf(F,df1=np5-np1,df2=N-np5),"\n")

Lo stesso risultato è riprodotto da

> anova(fit1,fit5) Analysis of Variance Table Model 1: loss ~ hard + tens Model 2: loss ~ hard + tens + I(tens^2) + I(tens^3) + I(tens^4) + I(tens^5) Res.Df RSS Df Sum of Sq F Pr(>F) 1 27 35950 2 23 12884 4 23065 10.294 6.286e-05 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Il modello M5 è dunque significativamente migliore di M1, come si può anche valutare visivamente dal confronto dei residui:

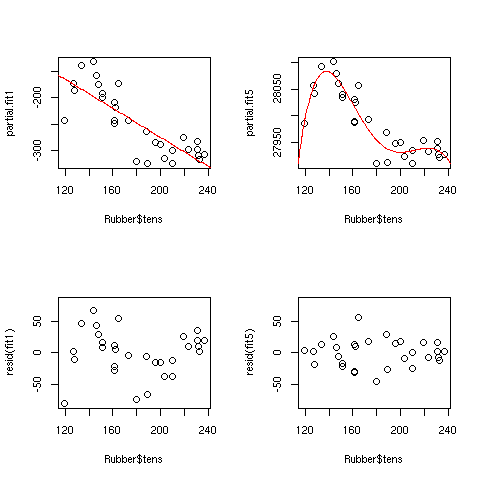
par(mfrow=c(2,2)) library(MASS) N=length(Rubber$loss) fit1=lm(loss~hard + tens,data=Rubber) fit5=lm(loss~hard + tens + I(tens^2) + I(tens^3)+ I(tens^4)+ I(tens^5),data=Rubber) partial.fit1=Rubber$loss - ( coef(fit1)[1] + coef(fit1)[2]*Rubber$hard) partial.fit5=Rubber$loss - ( coef(fit5)[1] + coef(fit5)[2]*Rubber$hard) plot( partial.fit1 ~ Rubber$tens) curve(coef(fit1)[3]*x,add=T,col="red" ) plot( partial.fit5 ~ Rubber$tens) curve(coef(fit5)[3]*x+coef(fit5)[4]*x^2+coef(fit5)[5]*x^3+coef(fit5)[6]*x^4+coef(fit5)[7]*x^5,add=T,col="red" ) plot(resid(fit1) ~ Rubber$tens,ylim=c(-80,80)) plot(resid(fit5) ~ Rubber$tens,ylim=c(-80,80)) par(mfrow=c(1,1))

Regressione lineare con variabili categoriali

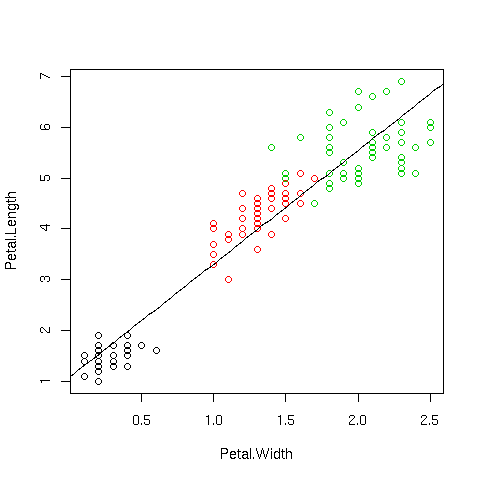
Supponiamo di voler modellizare la dipendenza della variabile dalla variabile per i dati nel dataframe iris. I dati suggeriscono una dipendenza lineare

$\displaystyle Petal.Length = \theta_0 + \theta_{1} Petal.Width + \epsilon$

plot(Petal.Length ~Petal.Width,data=iris,col=palette()[iris$Species]) lm1=lm(Petal.Length ~ Petal.Width,data=iris) cf=coef(lm1) curve(cf[1]+cf[2]*x,add=T)

Possiamo ora cercare di migliorare il modello tenendo conto di una eventuale dipendenza dei parametri dalla specie (si noti l'argomento $col=palette()[iris\$Species]$ della funzione che permette di disegnare i punti con colore diverso a seconda della specie).

Le funzioni di R permettono di eseguire un fit in cui uno o più parametri possono dipendere da una variabile categoriale (factor). Possiamo dunque far dipendere $\theta_0$ o $\theta_1$ dalla specie:

plot(Petal.Length ~ Petal.Width,data=iris,col=palette()[iris$Species]) # intercetta comune, pendenza dipendente dalla specie lm2=lm(Petal.Length ~ 1 + Species:Petal.Width,data=iris) cf=lm2$coefficients curve(cf[1]+cf[2]*x,add=T,col=1) curve(cf[1]+cf[3]*x,add=T,col=2) curve(cf[1]+cf[4]*x,add=T,col=3) # pendenza comune, intercetta dipendente dalla specie lm3=lm(Petal.Length ~ Species - 1 + Petal.Width,data=iris) cf=lm3$coefficients curve(cf[1]+cf[4]*x,add=T,col=1,lty=2) curve(cf[2]+cf[4]*x,add=T,col=2,lty=2) curve(cf[3]+cf[4]*x,add=T,col=3,lty=2)

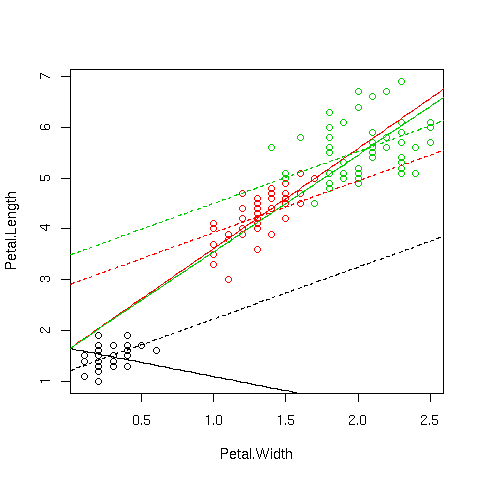
(si noti la sintassi Species - 1 per ottenere un'intercetta $(\theta_0)_j (j=1,3)$ dipendente dalla specie. Se avessimo omesso il termine -1, R avrebbe aggiunto un'intercetta comune e il risultato sarebbe stato equivalente, ma i parametri del fit sarebbero stati $(\theta_0)_1,((\theta_0)_2-(\theta_0)_1),((\theta_0)_3-(\theta_0)_1)$ .)

L'analisi della varianza ci suggerisce che per entrambi i modelli e , l'aggiunta di 2 parametri rispetto al modello lm1 è giustificata

> anova(lm1,lm2) Analysis of Variance Table Model 1: Petal.Length ~ Petal.Width Model 2: Petal.Length ~ 1 + Species:Petal.Width Res.Df RSS Df Sum of Sq F Pr(>F) 1 148 33.845 2 146 25.563 2 8.282 23.65 1.267e-09 *** --- > anova(lm1,lm3) Analysis of Variance Table Model 1: Petal.Length ~ Petal.Width Model 2: Petal.Length ~ Species - 1 + Petal.Width Res.Df RSS Df Sum of Sq F Pr(>F) 1 148 33.845 2 146 20.833 2 13.011 45.591 4.137e-16 ***

e fra i due il modello è evidentemente il migliore, avendo una minore $\sum (y_i-\lambda_i)^2$ a parità di gradi di libertà.

Possiamo infine far dipendere entrambi i parametri dalla specie (equivalente a fare 3 fits indipendenti per ciascuna specie)

plot(Petal.Length ~ Petal.Width,data=iris,col=palette()[iris$Species]) # pendenza e intercetta dipendente dalla specie lm4=lm(Petal.Length ~ Species - 1 + Species:Petal.Width,data=iris) cf=lm4$coefficients curve(cf[1]+cf[4]*x,add=T,col=1,lty=3) curve(cf[2]+cf[5]*x,add=T,col=2,lty=3) curve(cf[3]+cf[6]*x,add=T,col=3,lty=3)

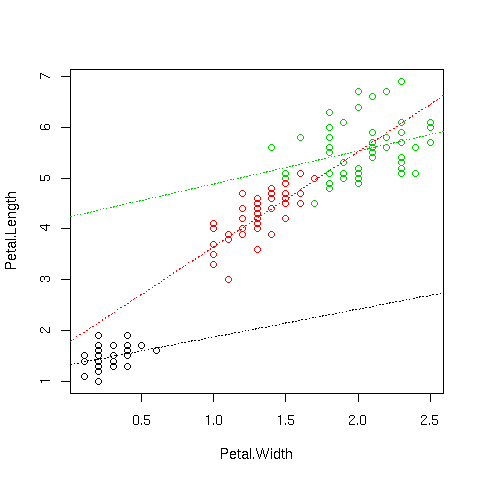
Anche in questo caso, i due parametri aggiuntivi sembrano giustificati:

> anova(lm3,lm4) Analysis of Variance Table Model 1: Petal.Length ~ Species - 1 + Petal.Width Model 2: Petal.Length ~ Species - 1 + Species:Petal.Width Res.Df RSS Df Sum of Sq F Pr(>F) 1 146 20.8334 2 144 18.8156 2 2.0178 7.7213 0.0006525 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Next: Minimi quadrati: Modelli lineari Up: Fits parametrici Previous: Fits parametrici

2008-05-30