Minimi quadrati: Modelli lineari generalizzati

Regressione logistica: i sopravvissuti del Titanic

Come esempio di modello lineare generalizzato, consideriamo i dati sulle frazioni di sopravvisuti all'incidente del Titanic, che ci aspettiamo seguire una distribuzione binomiale con probabilità di sopravvivenza $p$. Utilizziamo la funzione di link canonica della distribuzione binomiale, che è la funzione logistica

$$l(p) = log\left(\frac{p}{1-p}\right)$$

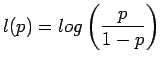
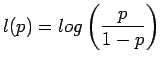
che parametrizziamo in funzione delle categorie di età, sesso, e classe di viaggio assumendo l'indipendenza dei 3 fattori:

$$l(p) = (\theta_{Age})_a + (\theta_{Sex})_s + (\theta_{Class})_c + \epsilon$$

dove
$a=Child,Adult$     $s=Male,Female$     $c=Class1nd,Class2nd,Class3nd,ClassCrew$

Possiamo eliminare la ridondanza dei parametri ponendo $(\theta_{Sex})_{Male}=(\theta_{Class})_{Class1nd}=0$.

# e' necessario modificare il dataframe per avere per ogni riga il numero di sopravvissuti
# e quello totale di ciascuna categoria
library(boot)
Tit=as.data.frame(Titanic)
c.vivi = Tit[Tit$Survived=="Yes","Freq"]
c.tutti = Tit[Tit$Survived=="No","Freq"] + c.vivi
NewTit=data.frame(Tit[Tit$Survived=="Yes",1:3],vivi=c.vivi,tutti=c.tutti)
#Eseguiamo il fit sulla frequenza vivi/tutti
logfit= glm(vivi/tutti ~  Age -1 +Sex+Class ,  weight=tutti,
       family=binomial,data=NewTit)
summary(logfit)

Dal risultato notiamo come tutti i parametri siano significativamente diversi da 0.

Per ottenere la probabilità di sopravvivenza ottenuta dal fit e il suo errore, usiamo la funzione $predict$ di R. Si noti l'opzione type="response" che ci permette di ottenere direttamente i valori di $p$ anzichè la quantità fittata $l(p)$:

> results=predict(logfit2,type="response",se.fit=T,newdata=NewTit)
> NewTit=data.frame(NewTit, prob.fit=results$fit,dprob.fit=results$se.fit)
> NewTit
   Class    Sex   Age vivi tutti     prob.fit  dprob.fit
17   1st   Male Child    5     5    0.6649249 0.06082307
18   2nd   Male Child   11    11    0.4175655 0.06533645
19   3rd   Male Child   13    48    0.2511586 0.04458132
20  Crew   Male Child    0     0    0.4570172 0.06370410
21   1st Female Child    1     1    0.9571141 0.01223942
22   2nd Female Child   13    13    0.8896612 0.02786822
23   3rd Female Child   14    31    0.7904463 0.04108526
24  Crew Female Child    0     0    0.9044523 0.02582406
25   1st   Male Adult   57   175    0.4070382 0.03286746
26   2nd   Male Adult   14   168    0.1987193 0.02474444
27   3rd   Male Adult   75   462    0.1039594 0.01182252
28  Crew   Male Adult  192   862    0.2254997 0.01405835
29   1st Female Adult  140   144    0.8853234 0.01704920
30   2nd Female Adult   80    93    0.7360897 0.03241455
31   3rd Female Adult   76   165    0.5661291 0.03175476
32  Crew Female Adult   20    23    0.7660538 0.02841769