Fits di Massima Verosimiglianza

Modello per i dati di un'eruzione

Il problema potrebbe essere risolto fittando l'istogramma della distribuzione della variabile $waiting$. La soluzione più generale possibile, che sfrutta interamente l'informazione disponibile, pena un maggiore dispendio di CPU, consiste tuttavia nello stimare i parametri massimizzando direttamente la funzione di likelihood del nostro campione

$$L(\alpha,\mu_1,\sigma_1,\mu_2,\sigma_2) = \prod_i f(w_i;\alpha,\mu_1,\sigma_1,\mu_2,\sigma_2)$$

Usiamo per questo la funzione $mle()$ del pacchetto $stats4$ che permette di minimizzare $-\log(L)$ con vari algoritmi di ottimizzazione. Scegliamo l'algoritmo "L-BFGS-B", che permette di definire dei limiti per i parametri del fit. Notiamo che nel nostro caso i parametri $(\mu_1,\sigma_1)$ e $(\mu_2,\sigma_2)$ possono facilmente essere ``scambiati'' (con un probabile fallimento della minimizzazione) se non rendiamo chiara la loro interpretazione scegliendo in modo sensato i valori di partenza e i limiti entro i quali eseguire la minimizzazione.

library(stats4)
geysermodel = function(x,alpha,mu1,sigma1,mu2,sigma2) {
alpha * dnorm(x,mean=mu1,sd=sigma1) +
   (1-alpha) * dnorm(x,mean=mu2,sd=sigma2)
}


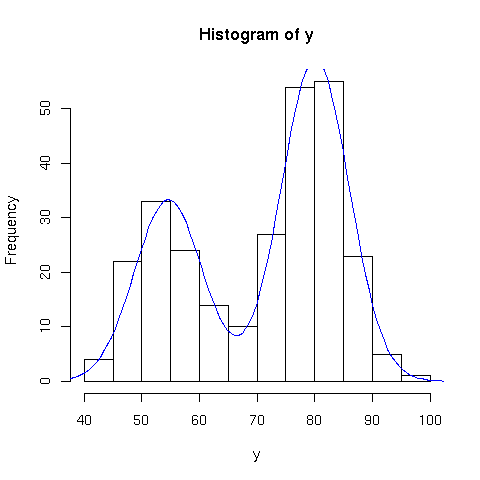
geyser.fit = function(y=faithful$waiting) {
 h=hist(y)
 startp=
   list(alpha=0.5,mu1=55,sigma1=5 ,mu2=80,sigma2=5)
 minp=c(alpha=0.1,mu1=45,sigma1=1 ,mu2=75,sigma2=1)
 maxp=c(alpha=0.9,mu1=60,sigma1=10,mu2=85,sigma2=10)
 
 llgeyser = function(alpha,mu1,sigma1,mu2,sigma2) {
  -sum(log(geysermodel(y,alpha,mu1,sigma1,mu2,sigma2)) )
 }

# l'argomento di mle deve essere una funzione che ritorna -logL
 fit=mle(llgeyser,start=startp,lower=minp,upper=maxp,method="L-BFGS-B")
 print(summary(fit))
 cf=fit@coef
 curve(geysermodel(x,cf[1],cf[2],cf[3],cf[4],cf[5]) * (h$breaks[2]-h$breaks[1]) * length(y),
   add=T,col="blue")
 list( min= fit@min , coef= cf, var=vcov(fit))
}

La funzione $geyser.fit$ così implementata ritorna una lista con i valori e la matrice var./cov. dei parametri, e il minimo ottenuto di $-\log(L)$.

> expfit = geyser.fit()
Maximum likelihood estimation

Call:
mle(minuslogl = llgeyser, start = startp, method = "L-BFGS-B", 
    lower = minp, upper = maxp)

Coefficients:
         Estimate Std. Error
alpha   0.3608887 0.03116472
mu1    54.6152983 0.69972712
sigma1  5.8715085 0.53739009
mu2    80.0912040 0.50459193
sigma2  5.8677196 0.40096112

-2 log L: 2068.004

Per poter eseguire un test di bontà del fit, è necessario conoscere la distribuzione attesa di $min(-\log(L))$ nell'ipotesi che il modello sia corretto.
Essendo un'impresa ardua determinare analiticamente questa distribuzione nel nostro caso (e questo vale per tutti i casi in cui la distribuzione $f(w)$ non sia particolarmente semplice), ricorriamo alla simulazione di $Nsim$ esperimenti con $n$ valori della nostra variabile simulati secondo la funzione $f(w)$:

geyser.check = function(Nsim=100) {
# inizializziamo un vettore che conterra' i valori di min(log(L)) di
# ogni esperimento simulato
 outll=c()
 n=length(faithful$waiting)
 for (i in 1:Nsim) {
# il numero di eventi del primo tipo segue una distribuzione binomiale 
# con prob. alpha
    n1=rbinom(1,size=n,prob=expfit$coef["alpha"])
    n2=n-n1
    sample=c( rnorm(n1,mean=expfit$coef["mu1"],sd=expfit$coef["sigma1"]) , 
              rnorm(n2,mean=expfit$coef["mu2"],sd=expfit$coef["sigma2"]) )
    simfit=geyser.fit(sample)
    outll[i]=simfit$min
 }
# distribuzione ottenuta dalla simulazione:
 hist(outll)
 cat("min logL =",expfit$min,"\n")
# disegniamo una linea verticale in corrispondenza del valore sperimentale
 lines(c(expfit$min,expfit$min),c(0,Nsim))
}

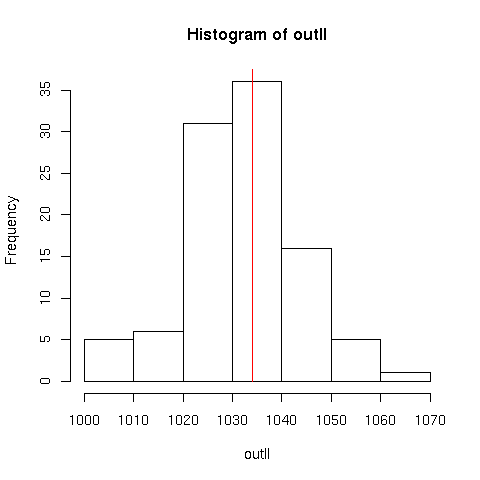
Come osserviamo dal grafico, il valore ottenuto sperimentalmente è perfettamente compatibile con il nostro modello.