Minimi quadrati: Modelli non lineari

Intensità di una sorgente radioattiva

Utilizziamo la funzione $nls$ di R per questa analisi di regressione non lineare. L'argomento $start$ deve contenere un vettore con i parametri liberi e il loro valore di partenza. Ogni parametro deve avere il nome che viene usato nella formula del modello. Nel nostro caso abbiamo un solo parametro che chiamiamo ``tau'':

mydata=read.table('/afs/math.unifi.it/service/Rdsets/decay.rdata')
plot(signal ~ time,data=mydata)
fit=nls(signal ~ exp(-time/tau), data=mydata,
	start=c(tau=2) )
lines(mydata$time,predict(fit))

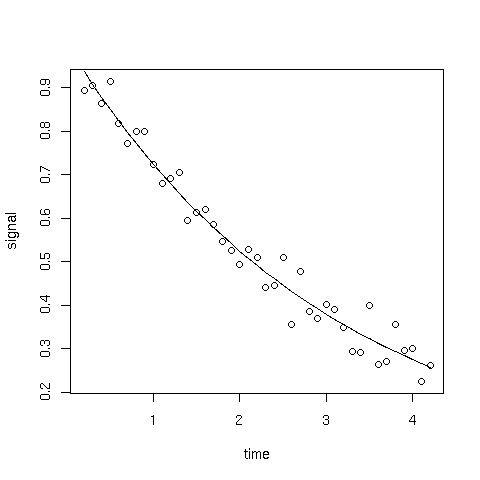
Dalla minimizzazione numerica del $\chi^2$ il fit ottiene
$\bar{\tau} = 3.10 \pm 0.06$

La variabile

$$t= (\bar{\tau}-\tau)/\bar{\sigma}_{\tau}$$

segue una distribuzione di Student con $N-1$ gradi di libertà, l'intervallo di confidenza è quindi

N=length(mydata$signal)
tau=fit$m$getPars()[1]
alpha=0.9
dtau=sqrt(vcov(fit)[1,1])
Nsigma = qt((1+alpha)/2,df=N-1)
cat ("tau=",tau," +/- ",Nsigma*dtau,"\n")

da cui
$\tau = 3.103 \pm 0.096$ al 90 % C.L.

L'intervallo di confidenza così ottenuto presuppone l'aver assunto una distribuzione di probabilità gaussiana per lo stimatore $\bar{\tau}$, cosa che nel caso non lineare è rigorosamente vera solo nel limite asintotico $N\to \infty$.

Per verificare questa approssimazione, confrontiamo il profilo del $\chi^2$ in funzione di $\tau$, con la predizione gaussiana

$$\chi^2(\tau) - \chi^2(\bar{\tau}) = 2 (\log(L(\bar{\tau})) -\log(L(\tau))) = \frac{(\tau-\bar{\tau})^2}{\bar{\sigma}^2_{\tau}}$$

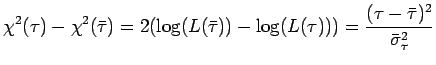
sigmay2=deviance(fit)/(N-1)

chi2.taufit = function(tau) {
 out=c()
 for (i in 1:length(tau) ) {
   out[i]=sum( ( mydata$signal - exp(-mydata$time/tau[i])   )^2  )/sigmay2
 }
 out
}

# profilo effettivo in nero
curve(chi2.taufit(x),tau-3*dtau,tau+3*dtau,
  xlab=expression(tau),ylab=expression(chi^2))
# predizione approssimato in rosso
curve((N-1)+(x-tau)^2/dtau^2,add=T,col="red")

Il plot dimostra la validità dell'approssimazione. Se infatti volessimo migliorare la stima dell'intervallo di confidenza, calcolando i valori di $\tau$ per cui $\chi^2 = min(\chi^2) + N_{\sigma}^2(\alpha)$, otterremmo
$\tau = 3.103 - 0.094 + 0.098$ al 90 % C.L.
con una variazione della stima degli errori di circa il 2 %.

Caso con due parametri

Ripetiamo il procedimento con due parametri liberi

mydata=read.table('/afs/math.unifi.it/service/Rdsets/decay.rdata')
plot(signal ~ time,data=mydata)
fit=nls(signal ~ I0*exp(-time/tau), data=mydata,
	start=c(I0=1,tau=2) )
print(summary(fit))
lines(mydata$time,predict(fit))

da cui si ottiene

Parameters:
    Estimate Std. Error t value Pr(>|t|)    
I0   1.00321    0.01757   57.09   <2e-16 ***
tau  3.08820    0.09752   31.67   <2e-16 ***

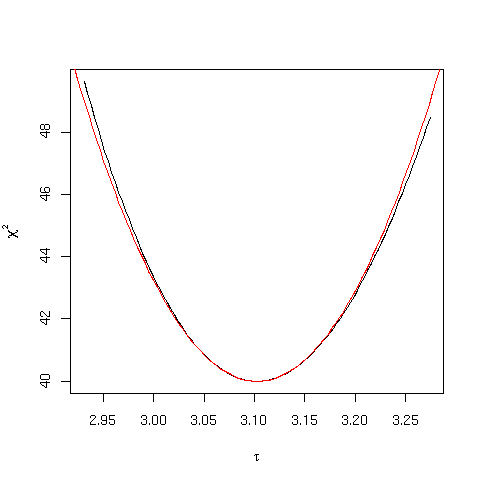
In questo caso, l'approssimazione gaussiana prevede che il profilo del $\chi^2$ sia dato dal logaritmo di una gaussiana bivariata

$$\chi^2(\tau,I_0) - \chi^2(\bar{\tau},\overline{I_0}) = (\theta - ... ...rho (\tau-\bar{\tau})(I_0-\overline{I_0})}{\sigma_{\tau}\sigma_{I_0}} \right]$$

N=length(mydata$signal)
theta=fit$m$getPars()
V.theta=vcov(fit)
dtau=sqrt(diag(vcov(fit)))
sigmay2=deviance(fit)/(N-2)

chi2.taufit2 = function(I0,tau) {
 out=matrix(nrow=length(I0),ncol=length(tau))
 for (i in 1:length(I0) ) {
  for (j in 1:length(tau) ) {
  out[i,j]=sum( ( mydata$signal - I0[i]*exp(-mydata$time/tau[j])   )^2  )/sigmay2
  }
 }
 out
}

pred.chi2.taufit2 = function(I0,tau) {
 out=matrix(nrow=length(I0),ncol=length(tau))
 for (i in 1:length(I0) ) {
  for (j in 1:length(tau) ) {
  xy=c(I0[i],tau[j])
  out[i,j]= (N-2) + t(xy-theta) %*% solve(V.theta)  %*% (xy-theta)
  }
 }
 out
}

nsigma=c(1,2,3)
x=seq(0.95,1.05,0.001)
y=seq(2.5,3.5,0.005)
# profilo effettivo in nero
contour(x,y, chi2.taufit2(x,y) ,  levels = (N-2) + nsigma^2,
 xlab=expression(I0),ylab=expression(tau))
# predizione approssimata in rosso
contour(x,y, pred.chi2.taufit2(x,y) ,  levels =(N-2) + nsigma^2,
col="red",add=T )

Analisi di una dieta

Essendo il modello non lineare, utilizziamo la funzione nls() con i tre parametri liberi

 library(MASS)
 plot(Weight ~ Days,data=wtloss)
 theta.start=c(W.0=100, W.e=100,D.half=200)
 fit=nls(Weight ~ W.0 + W.e * 2^(-Days/D.half) , data=wtloss, start=theta.start)
 print(summary(fit))
 lines(wtloss$Days,predict(fit),col="blue")

# matrice di correlazione fra i parametri
 Vcor = cov2cor(vcov(fit))
 rho = Vcor["W.0","W.e"]
 ngl=length(wtloss$Weight)-3
 drho =  (1-rho^2)/sqrt(ngl)
 cat("rho(W.0,W.e)=",round(rho,3)," +/- ",round(drho,3),"\n")

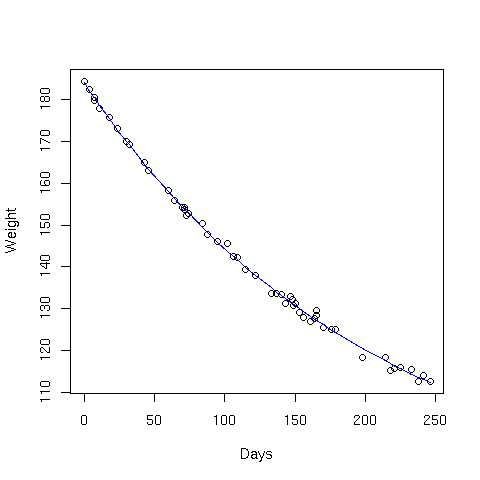
Da cui otteniamo

Parameters:
       Estimate Std. Error t value Pr(>|t|)    
W.0      81.374      2.269   35.86   <2e-16 ***
W.e     102.684      2.083   49.30   <2e-16 ***
D.half  141.910      5.295   26.80   <2e-16 ***

rho(W.0,W.e)= -0.989  +/-  0.003

Test del modello

Supponendo che la deviazione standard di ogni misura sia determinata dalla precisione della bilancia $\sigma=0.5$ Kg, possiamo calcolare il $\chi^2$ del fit ed eseguire un test dell'ipotesi che segua una distribuzione di Pearson con $N-3$ gradi di libertà:

> chi2=deviance(fit)/0.5^2
> cat("chi2=",chi2," con ",ngl," g.d.l. : p-value=",
      1-pchisq(chi2,df=ngl),"\n")
chi2= 156.9788  con  49  g.d.l. : p-value= 3.100853e-13

Evidentemente l'errore nella misura non basta a spiegare la varianza dei residui del fit, che probabilmente è dominata da fluttuazioni fisiologiche del peso, e magari da qualche strappo alla dieta!