Data l'indipendenza degli eventi, il numero di conteggi

Data l'indipendenza degli eventi, il numero di conteggi ![]() misurato
in ogni intervallo seguirà una
distribuzione di Poisson con valore atteso pari a
misurato
in ogni intervallo seguirà una
distribuzione di Poisson con valore atteso pari a
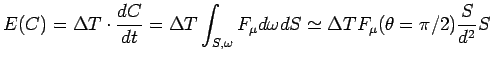
|
(abbiamo trascurato le dimensioni lineari dei rivelatori rispetto a
|
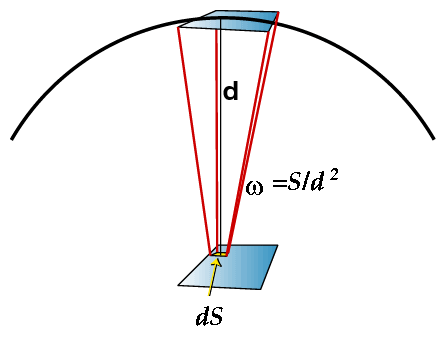 |
![]() è dunque semplicemente proporzionale al valore atteso della
distribuzione, che può essere stimato correttamente e nel modo più
efficiente dalla media aritmetica
è dunque semplicemente proporzionale al valore atteso della
distribuzione, che può essere stimato correttamente e nel modo più
efficiente dalla media aritmetica
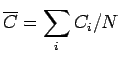
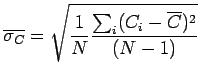
Il seguente codice risolve il problema:
# creaiamo un dataframe dal file
# l'opzione skip permette di saltare le prime righe
# di spiegazione nel file
df = read.table(file="/afs/math.unifi.it/service/Rdsets/CosmoData.txt",skip=7)
c = df$V3
n=length(c)
d=47 # cm
S=251.7 # cm^2
deltaT=2 # minutes
cm=mean(c) # etc..
dcm=sqrt(var(c)/n)
cat("average counts is ",cm," +/- ",dcm,"\n")
k=(d/S)^2/deltaT
cat("flux is ",cm*k," +/- ",dcm*k," muons/cm^2/sterad/min\n")
|
Naturalmente avremmo potuto considerare la somma di tutti i conteggi
come un unico conteggio corrispondente ad un intervallo
![]() . In tal caso la media coincide con l'unico valore misurato
. In tal caso la media coincide con l'unico valore misurato
![]() e il risultato per il flusso resta invariato. Sapendo
che la varianza della distribuzione di Poisson è uguale al valore
atteso, il valore
e il risultato per il flusso resta invariato. Sapendo
che la varianza della distribuzione di Poisson è uguale al valore
atteso, il valore ![]() è anche uno stimatore della varianza. L'errore
standard su
è anche uno stimatore della varianza. L'errore
standard su ![]() è dunque semplicemente
è dunque semplicemente ![]() .
.
L'aver suddiviso i conteggi in ![]() intervalli ci permette comunque di
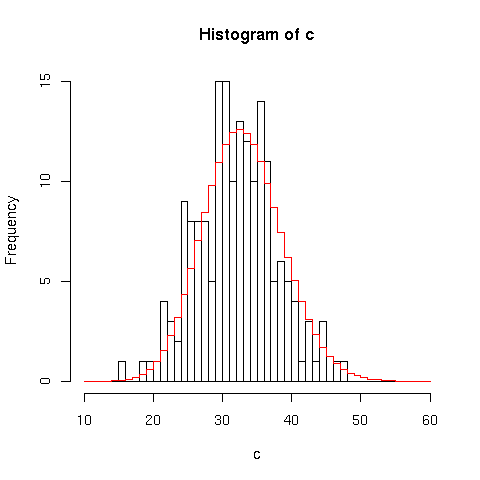
verificare l'ipotesi poissoniana:
intervalli ci permette comunque di
verificare l'ipotesi poissoniana:
x=10:60 hist(c,breaks=x) points(x,dpois(x,lambda=cm)*n,type="s",col="red") |