Stimatori di massima verosimiglianza

Vita media di un decadimento radioattivo

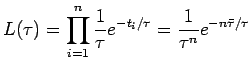
La funzione di likelihood è

$$L(\tau) = \prod_{i=1}^{n} \frac{1}{\tau} e^{-t_i/\tau} = \frac{1}{\tau^n} e^{-n\bar{\tau}/\tau}$$

dove $\bar{\tau}=\sum_i t_i/n$ è la media aritmetica delle misure.

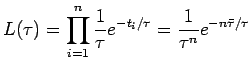
Lo stimatore di massima verosimiglianza $\bar{\tau}_{ML}$ si ottiene da

$$\left. \frac{\partial logL}{\partial \tau}\right\vert _{\tau=\bar{\tau}_{ML}} = 0$$

$$-\frac{n}{\bar{\tau}_{ML}} + \frac{n\bar{\tau}}{\bar{\tau}_{ML}^2} = 0      \Longrightarrow      \bar{\tau}_{ML} = \bar{\tau}$$

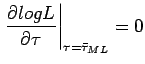
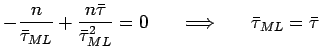
Lo stimatore ML coincide dunque con la media aritmetica che è uno stimatore corretto del valore atteso $\tau$ ed ha varianza

$$\sigma^2(\bar{\tau}) = \sigma^2(t)/n = \tau^2 / n$$

L'informazione di Fisher è

$$I(\tau) = E\left( \left( \frac{\partial \log{L}}{\partial \tau} \... ...tau^2}\left( \frac{\tau^2}{n}+\tau^2 \right) -2 +1 \right] = \frac{n}{\tau^2}$$

e l'efficienza è dunque

$$\epsilon(\bar{\tau}) = \frac{1}{\sigma^2(\bar{\tau}) I(\tau)} = 1$$

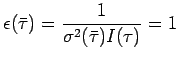
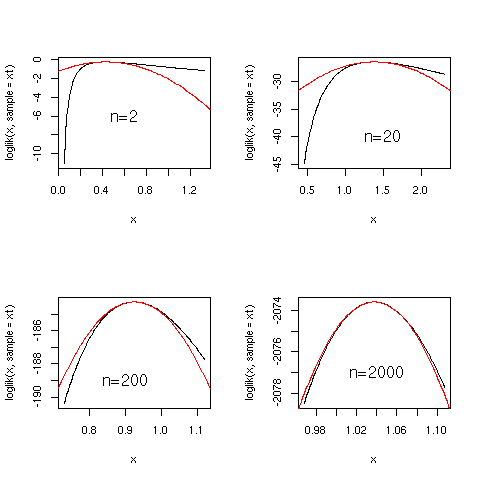
Con il seguente codice verifichiamo che il limite asintotico ( $n\to\infty$) della funzione di lihelihood è

$$\log{L}(\tau) \to \log{L}(\bar{\tau}) - \frac{(\tau-\bar{\tau})^2}{2} I(\tau) = \log{L}(\bar{\tau}) - \frac{n(\tau-\bar{\tau})^2}{2\bar{\tau}^2}$$

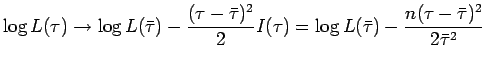
loglik = function (tau,sample) {
 n=length(sample)
 etau=mean(sample)
 -n*(log(tau)+etau/tau)
}

seelik = function(n=1000) {
xt=rexp(n)
etau=mean(xt)
detau=etau/sqrt(n)
cat("tau estimate is ",etau," +/- ",detau,"\n")
curve(loglik(x,sample=xt),max(etau-3*detau,0.05),etau+3*detau)
curve(loglik(etau,sample=xt)-(x-etau)^2/(2*detau^2),add=T,col="red")
}

par(mfrow=c(2,2))
seelik(2)
seelik(20)
seelik(200)
seelik(2000)

Segnale con fondo uniforme

Parametrizziamo la distribuzione di probabilità della variabile misurata, l'energia x:

$$f(x;\mu,\alpha) = (1-\alpha) \phi_{Gauss}(x;\mu,\sigma_G) + \alpha d_{unif}(x;x_{min},x_{max})$$

dove $\sigma_G=0.3$ MeV, $x_{min}=0$, $x_{min}=10$ MeV.

Una prima stima dei parametri $\mu$ e $\alpha$ può essere ottenuta stimando il valore atteso e la varianza della distribuzione:

$$\begin{split}E(x) & = \int x f(x) dx = (1-\alpha) \int x \phi... ...d_{unif}(x) dx = & = (1-\alpha) \mu + \alpha E_u \end{split}$$

$$\begin{split}\sigma^2(x) & = E(x^2) - E(x)^2 = (1-\alpha) \in... ...^2 \simeq (1-\alpha) \sigma_G^2 + \alpha \sigma_u^2 \end{split}$$

dove $E_u = 5 MeV$ e $\sigma_u^2 = 100/12$ MeV$^2$ sono il valore atteso e la varianza della distribuzione uniforme, e si è ottenuta l'ultima relazione assumendo $\vert\mu-E_u\vert« \sigma_u^2$.

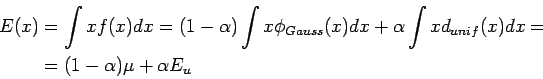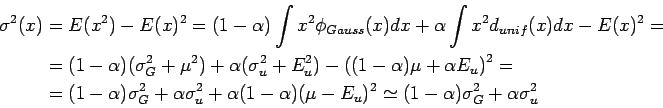Ricaviamo dunque gli stimatori

$$\bar{\alpha} = \frac{\overline{\sigma^2(x)}-\sigma_G^2}{\sigma_u^2-\sigma_G^2}$$

$$\bar{\mu} = \frac{\overline{E(x)}-E_u \cdot \bar{\alpha}}{1-\bar{\alpha}}$$

usando i noti stimatori corretti di $E(x)$ e $\sigma^2(x)$

$$\bar{x} = \overline{E(x)} = \sum_i x_i/N$$

$$\overline{\sigma^2 (x)} = \sum_i ( x_i - \bar{x} )^2 /(N-1)$$

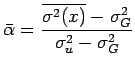
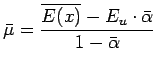
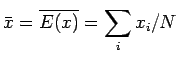
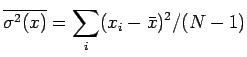
Gli errori standard su queste stime saranno:

$$\sigma(\bar{\alpha}) = \frac{\overline{\sigma_G(\overline{\sigma^2(x)})}}{\sigma_u^2-\sigma_G^2}$$

$$\sigma(\bar{\mu}) \simeq \frac{\overline{\sigma_G(\overline{E(x)}... ...bar{\alpha}} = \frac{1}{1-\bar{\alpha}}\sqrt{\frac{\overline{\sigma^2(x)}}{N}}$$

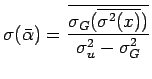
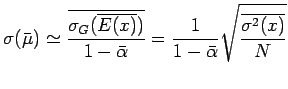
dove abbiamo trascurato l'incertezza su $\bar{\alpha}$ nell'espressione di $\sigma(\bar{\mu})$ e

$$\overline{\sigma_G(\overline{\sigma^2(x)})} = \sqrt{\frac{1}{N}\l... ...right)} \simeq \sqrt{\frac{\overline{\mu_4(x)} - \overline{\sigma^2(x)}^2}{N}}$$

$$\overline{\mu_4(x)} = \frac{\sum_i (x_i - \bar{x})^4}{N-1}$$

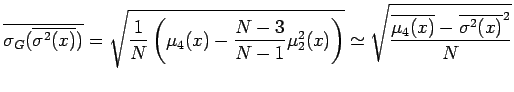
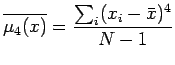
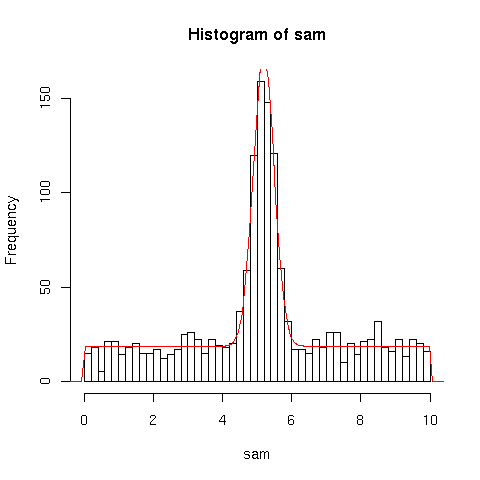
Stimiamo i valori numerici e verifichiamo graficamente il risultato:

gaussconfondo= function(x,alpha,mu,s1=0.3) {
 (1-alpha)*dnorm(x,mean=mu,sd=s1)+alpha*dunif(x,min=0,max=10)
}

> sam=scan("gaussconfondo.rdata")
> n=length(sam)
> s1=0.3
> myalpha=(var(sam)-s1^2)/(25/3-s1^2)
> mu4=mean((sam-mean(sam))^4)
> dvar=sqrt((mu4-var(sam)^2)/n)
> mydalpha=dvar/(25/3-s1^2)

> mymu=(mean(sam)-5*myalpha)/(1-myalpha)
> mydmu = sqrt(var(sam)/(n*(1-myalpha)^2))

> cat ("stima di alpha: ",myalpha," +/- ",mydalpha,"\n")
stima di alpha:  0.5873126  +/-  0.02139240 
> cat ("stima di mu: ",mymu," +/- ",mydmu,"\n")
stima di mu:  5.433121  +/-  0.1383849

hist(sam,breaks=seq(0.,10.,0.2))
curve(gaussconfondo(x,alpha=myalpha,mu=mymu)*n*0.2,add=T,col="red")

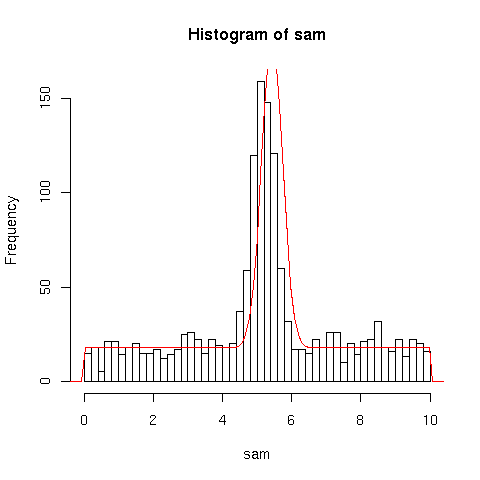
E' evidente che la stima di $\mu$, seppur corretta entro l'errore stimato, può essere migliorata. Questo non è sorprendente dal momento che, usando la media aritmetica, abbiamo utilizzato con lo stesso peso tutti gli eventi, anche quelli del fondo che non portano alcuna informazione su $\mu$ ma aggiungono solo ``rumore'' alla nostra stima. Il metodo di ML ci fornisce invece uno stimatore che estrae dai dati il massimo dell'informazione. Ci aspettiamo inoltre che, vista la statistica relativamente elevata del campione, lo stimatore abbia alta efficienza e bias trascurabile.
Calcoliamo il massimo della funzione di likelihood numericamente minimizzando la quantità $-\log{L}$. In generale, dovremmo trovare il minimo variando simultaneamente i due parametri $\mu$ e $\alpha$. Tuttavia ci aspettiamo che la correlazione fra i due parametri sia piccola, poichè i parametri descrivono caratteristiche diverse del campione. E' dunque ragionevole stimare un parametro alla volta, ed eventualmente raffinare la stima procedendo in modo iterativo:

loglikgfa = function(a,sample,m) {
 out=c()
 for (i in 1:length(a)) {
  out[i] = -sum(log(gaussconfondo(sample,alpha=a[i],mu=m)))
 }
 out
}

loglikgfmu = function(m,sample,a) {
 out=c()
 for (i in 1:length(m)) {
  out[i] = -sum(log(gaussconfondo(sample,alpha=a,mu=m[i])))
 }
 out
}

# prima stima di mu e alpha
curve(loglikgfmu(x,sam,myalpha),5.15,5.25)
# possiamo stimare visivamente dal grafico
# mu_ML = 5.192 +/- 0.016

curve(loglikgfa(x,sam,mymu),0.5,0.7)
# possiamo stimare visivamente dal grafico
# alpha_ML = 0.650 +/- 0.015

# seconda iterazione
curve(loglikgfmu(x,sam,0.650),5.17,5.21,xlab=expression(mu))
curve(loglikgfa(x,sam,5.192),0.55,0.65,xlab=expression(alpha))

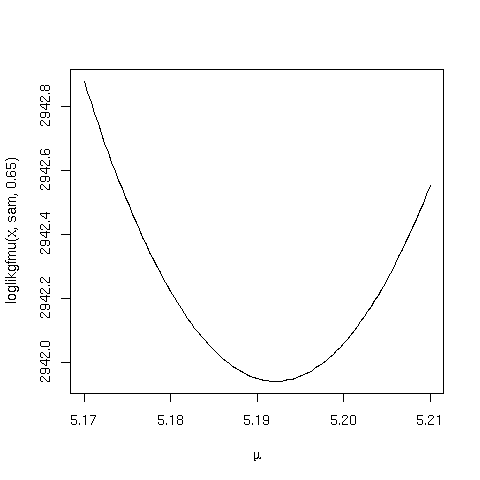
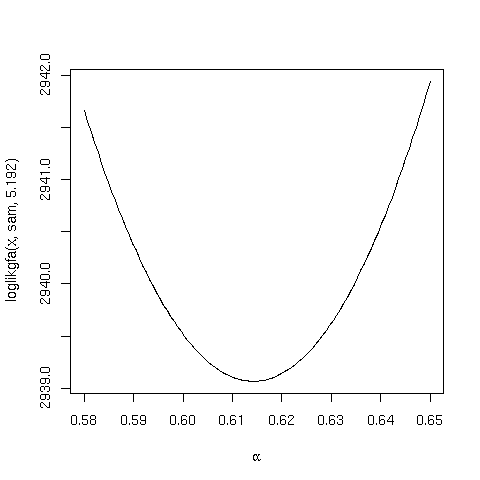
Dai grafici possiamo stimare, valutando i valori per cui $-\log{L}$ differisce di 1/2 dal minimo:

$$\bar{\mu}_{ML} = 5.192 \pm 0.016$$

$$\bar{\alpha}_{ML} = 0.614 \pm 0.015$$

Una ulteriore iterazione non produce variazioni rivelanti. Come ci si poteva aspettare, la precisione della nostra stima è decisamente migliorata, in particolare per $\mu$. Notiamo anche come il profilo di $\log{L}$ sia parabolico, confermandoci che siamo prossimi al limite asintotico in cui gli stimatori di ML sono corretti ed efficienti.
In effetti, il campione considerato è stato simulato con i valori $\mu=5.2$, $\alpha=0.6$, in perfetto accordo con le nostre stime.

Con un maggior dispendio di CPU avremmo potuto minimizzare la funzione in due dimensioni utilizzando l'apposita funzione di R $mle()$, che permette di scegliere fra vari algoritmi di minimizzazione. La procedura è la seguente:

# e' necessario specificare i valori di partenza dei parametri e 
# gli intervalli entro cui cercare il minimo
minusll = function(mu=5.4,alpha=0.65) {
 -sum(log(gaussconfondo(sam,alpha=alpha,mu=mu)))
}

> library(stats4)
> mle(minusll,method="L-BFGS-B",lower=c(5.0,0.5),upper=c(5.4,0.7)) -> fit
> summary(fit)
Maximum likelihood estimation

Call:
mle(minuslogl = minusll, method = "L-BFGS-B", lower = c(5, 0.5), 
    upper = c(5.4, 0.7))

Coefficients:
        Estimate   Std. Error
mu    5.1918609   0.01579727
alpha 0.6142559   0.01498571

-2 log L: 5878.132

Come previsto, abbiamo ritrovato i valori ottenuti ``manualmente''.

La funzione $mle()$ è in grado di stimare la matrice varianza/covarianza dei due stimatori valutando numericamente

$$(V_{\theta}^{-1})_{i,j} = \left( \left. \frac{\partial^2 \log(L)... ...ial \theta_i \partial \theta_j}\right\vert _{\theta=\bar{\theta}} \right)_{i,j}$$

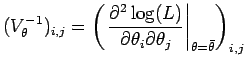
> vcov(fit)
                mu          alpha
mu    2.495537e-04   1.617870e-06
alpha 1.617870e-06   2.245715e-04
# in termini di coefficienti di correlazione:
> cov2cor(vcov(fit))
               mu         alpha
mu    1.000000000    0.006834148
alpha 0.006834148    1.000000000

Otteniamo dunque un coefficiente di correlazione inferiore all'1 %.

Verifichiamo infine graficamente l'accordo fra i dati e la miglior stima ottenuta:

hist(sam,breaks=seq(0.,10.,0.2))
curve(gaussconfondo(x,alpha=0.614,mu=5.192)*n*0.2,add=T,col="red")