Cosa sono?
Cosa sono? Gli sviluppi di numeri razionali
Gli sviluppi di numeri razionali I convergenti
I convergenti Gli sviluppi dei numeri irrazionali
Gli sviluppi dei numeri irrazionali Bibliografia
Bibliografia
Consideriamo l'equazione:
Ricavando la x dal termine di secondo grado si ha:
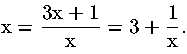
Sostituiamo alla x al secondo membro il valore appena ricavato:
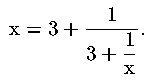
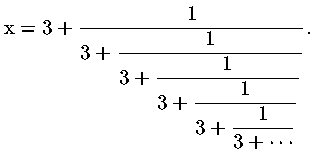
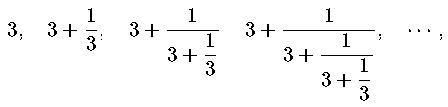
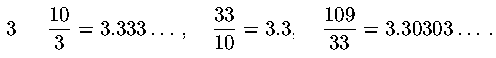
La radice positiva dell'equazione vale invece:
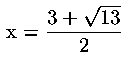
che coincide, se arrotondata alla terza cifra decimale, con il valore
dell'ultimo convergente riportato (cioè il convergente fornisce un
valore della radice dell'equazione con 3
cifre esatte).
I calcoli fatti suggeriscono un paio di domande:
In generale, una frazione continua è una espressione del tipo
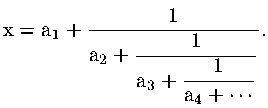
Esempio: 67/29 = [2, 3, 4, 2].Avremo anche potuto scrivere 67/29 = [2, 3, 4, 1, 1] (basta sostituire il 2 finale con 1+1/1). Questo ci permette di enunciare il teorema seguente:
Come si arriva al risultato? Dividendo 67 per 29 si ottiene 2 con resto 9. Quindi:Se ora dividiamo 29 per 9 si ottiene 3 con resto 2. Quindi, sostituendo:
Proseguendo finché non si ottiene resto zero si arriva al risultato.
Teorema: Ogni razionale si può scrivere in frazione continua sia con un numero pari che con un numero dispari di quozienti, modificando soltanto l'ultimo termine.Questo teorema sarà utile per risolvere le equazioni diofantee.
Dalle divisioni successive per sviluppare un razionale p/q in frazione continua si ottengono le equazioni:
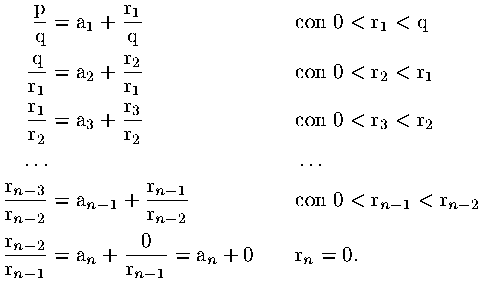
È interessante osservare che le equazioni scritte sono le stesse che figurano nell'algoritmo euclideo per il calcolo del massimo comune divisore tra due numeri p e q.
3. I convergenti.
Se p/q = [a1, a2, ..., an, ...], le
quantità
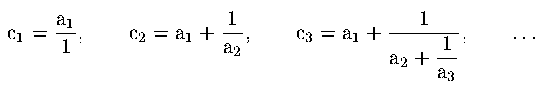
sono dette convergenti della frazione continua. L'ultimo
convergente è uguale alla frazione stessa.
Dato che i convergenti sono essi stessi frazioni, possiamo porre che i convergenti godono della seguente
proprietà:
Teorema dei convergenti: Se ci = pi / qi, allora piqi-1 - pi-1qi = (-1)i.Il teorema si dimostra utilizzando il principio di induzione e la relazione di ricorrenza che lega tra loro i convergenti:
per i = 3, 4, 5, ..., con i valori iniziali
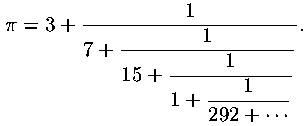
Come si ottengono questi sviluppi? Fino ad ora abbiamo determinato i
quozienti prendendo il quoziente di una divisione, mentre il resto era il
punto di partenza per calcolare il quoziente successivo.
Ora però non abbiamo più a che fare con razionali, quindi non
abbiamo più a disposizione un numeratore e un denominatore per fare la
divisione. Basta però accorgersi che quello che facevamo non era altro
che prendere come quoziente la parte intera del valore decimale della
frazione e come resto la parte decimale. I primi termini dello
sviluppo del numero e, base dei logaritmi naturali, sono:
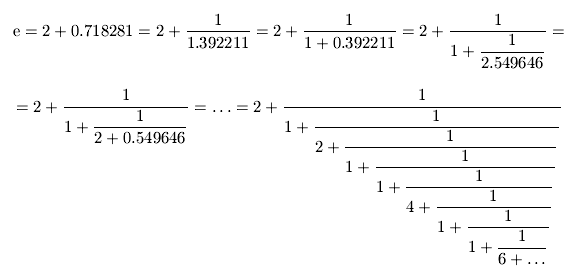
I numeri della forma
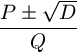
ovvero le soluzioni delle equazioni del tipo Q2x2 - 2PQx + (P2 - D) = 0, sono detti irrazionali quadratici. Hanno la caratteristica di avere lo sviluppo in frazione continua periodica; ad esempio, ricordando quanto detto all'inizio del primo paragrafo si vede subito che
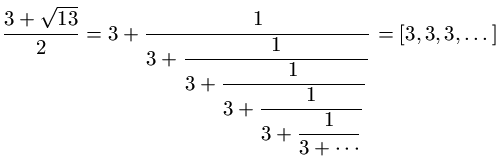
Non è detto che gli sviluppi siano periodici puri: può anche essere presente una parte di antiperiodo, come ad esempio per
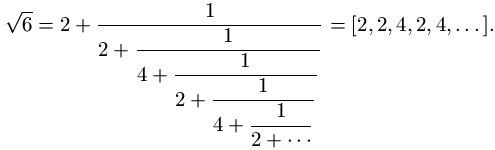
Il valore di una frazione continua periodica pura può essere calcolato facilmente utilizzando al contrario il procedimento utilizzato per calcolarla. Facendo riferimento al solito esempio di [3, 3, 3, ... ], basta osservare che se x è il valore della frazione continua, poiché il denominatore della prima frazione è la frazione stessa, deve valere la relazione
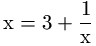
da cui si vede che x è la soluzione positiva dell'equazione
x2 - 3x - 1 = 0.
In maniera simile si calcola il valore delle altre frazioni continue
periodiche: consideriamo la frazione x = [2, 2, 4, 2, 4, ...].
Calcoliamo innanzitutto il valore della sua parte periodica utilizzando
la tecnica appena vista:
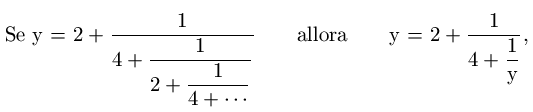
Sostituendo poi il valore ottenuto nella frazione originaria ne possiamo calcolare il valore: