Francesco Mugelli

Il principio di induzione.

Il principio di induzione matematica non è un argomento di ricerca; è invece uno strumento che i matematici hanno a disposizione per fare ricerca. In molte dimostrazioni ne viene fatto uso, dalle più semplici alle più complesse.

Supponiamo di dover dimostrare che una certa proprietà è vera per tutti i membri di un insieme con infiniti elementi. Tanto per fissare le idee immaginiamo che l'insieme sia quello dei numeri naturali. Potremmo cominciare a dimostrare che vale per il primo elemento, poi per il secondo, per il terzo e così via ma, dato che ci sono infiniti elementi, non arriveremmo mai in fondo.
Potremmo cercare di scrivere la proprietà in una forma che vada bene per tutti gli elementi e dimostrarla direttamente, ma questo non sempre è facile, anche perché potremmo avere a che fare con proprietà definite per ricorrenza.
L'efficacia del principio di induzione si vede soprattutto in quest'ultimo caso. Facciamo un semplice esempio:

Supponiamo di voler dimostrare che

Per ogni valore di n dobbiamo dimostrare un'uguaglianza. Supponiamo di aver gia dimostrato l'uguaglianza per tutti gli interi n minori di un certo valore. Come possiamo fare per dimostrarla per il valore successivo senza rifare tutta la somma da capo? Basta aggiungere l'ultimo addendo alla somma già fatta!
Nel nostro caso potremo scrivere:

E se ora volessimo dimostrare la proprietà per il valore ancora successivo? Basterebbe ripetere lo stesso procedimento. E per n+100000? Andrebbe ripetuto 100000 volte, ma sempre lo stesso.

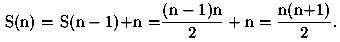
Il principio di induzione matematica si basa proprio su questo: per dimostrare una proprietà Pn per ogni valore di n, basta provarla esplicitamente per il primo valore (questo nell'esempio corrisponde ad osservare che S(1) = ((1+1)*1)/2 = 1 ), e poi, supponendo che la proprietà valga per un certo valore n - 1 dell'indice, dimostrare che vale per il valore successivo n, cioè dimostrare che Pn-1 implica Pn.
Se volessimo dimostrare per esempio che P5 è vera, osserviamo prima di tutto che è vera P1. Poi, dato che Pn - 1 implica Pn segue che è vera anche P2. Ma allora, ripetendo lo stesso ragionamento, è vera anche P3 e così via fino ad arrivare a P5. Con questo ragionamento si può raggiungere con un numero finito di passi, cioè con un procedimento che ha termine, qualunque valore di n, ovvero possiamo affermare che Pn è vera per ogni valore di n.