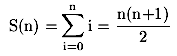
Una successione famosa

Francesco Mugelli

Una successione, una proprietà ecc. dipendente da un indice è definita per ricorrenza se è definita riferendosi ai valori precendenti dell'indice e non esplicitamente.
Per esempio, la successione

a₁ = 3, a₂ = 4, a₃ = 6, a₄ = 10, a₅ = 18, a₆ = 34, ecc.

può anche essere definita per ricorrenza se assegnamo un valore iniziale ed una legge per ricavare un termine in base ai precedenti:

a₁ = 3, a_n = 2 a_{n - 1} - 2.

Una sommatoria può sempre essere scritta come una ricorrenza. Nel nostro esempio,

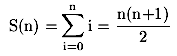
il valore iniziale è S(1) = 1 e la legge è S(n) = S(n - 1) + n.

Una successione famosa, definita per ricorrenza è la successione di Fibonacci, in cui la ricorrenza è fatta utilizzando due termini invece di uno solo. Di conseguenza sarè necessario assegnare due valori iniziali:

a₁ = 1, a₂ = 1, a_n = a_{n - 1} + a_{n - 2}.

I primi termini di questa successione sono:

a₃ = 2, a₄ = 3, a₅ = 5, a₆ = 8, a₇ = 13, a₈ = 21, a₉ = 34, ecc.

La successione diverge ad infinito. Se consideriamo invece il rapporto q_n = a_n / a_{n - 1} tra due termini successivi, i primi valori di q_n sono:

q₂ = 1/1 = 1.0000	q₆ = 8/5 = 1.6666
q₃ = 2/1 = 2.0000	q₇ = 13/8 = 1.6250
q₄ = 3/2 = 1.5000	q₈ = 21/13 = 1.6154
q₅ = 5/3 = 1.6666	q₉ = 34/21 = 1.6190

Il rapporto tra due termini successivi tende ad un certo valore L. Siete in grado di calcolare esattamente L? Forse informandovi sulle frazioni continue potrebbe venirvi qualche idea. Ci sono comunque anche altri modi, forse più semplici, di trovare la soluzione.