Test di Student

Confronto fra distribuzioni di Student e di Gauss

Il seguente codice permette di visualizzare la differenza fra la distribuzione di Student e la distribuzione normale standard in funzione del numero di gradi di libertà.

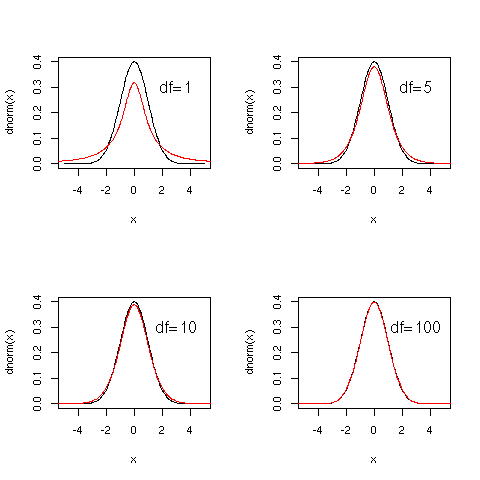
seestudent= function(df=1) {
 curve(dnorm(x),-5,5)
 curve(dt(x,df=df),add=T,col="red")
}

Il classico test sull'effetto dello hyoscyamine hydrobromide

Assumendo che la risposta dei pazienti segua una distribuzione normale con media e deviazione standard incognite, la variabile empirica

$$t = \frac{(\overline{x}-\lambda_0)}{\overline{\sigma_{\overline{x}}}}$$

(dove $\overline{x}$ e $\overline{\sigma_{\overline{x}}}$ sono gli stimatori della media e del suo errore, e $\lambda_0=0$ è il valore atteso nell'ipotesi nulla)
seguirà una distribuzione di Student con $10-1$ gradi di libertà.

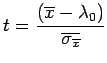
Assumendo che l'ipotesi alternativa consista in un incremento significativo delle ore di sonno, possiamo eseguire il test di Student ad una coda calcolando dunque il p-value come la probabilità di ottenere un valore di $t$ superiore o uguale a quello misurato.
Il seguente codice, oltre ad eseguire il test calcolando il p-value, calcola il limite inferiore per il valore atteso dell'effetto del sonnifero, e mostra il risultato graficamente.

ttestsleep = function(gr=1,conflevel=0.95) {
 m=subset(sleep,group==gr)$extra
 hist(m,xlab=paste("Extra-sleep case ",gr))
 n=length(m)
 ngl=n-1
 dmean=sd(m)/sqrt(n)
 t=mean(m)/dmean
 cat(" test di compatibilità con 0 (1 coda): pvalue=",(1-pt(t,df=ngl)),"\n")
 nsigma=qt((1+conflevel)/2,df=ngl)
 limite=mean(m)-dmean*qt(conflevel,df=ngl)
 cat("  limite: >",limite," per livello di confidenza=",conflevel,"\n")
 lines(c(limite,limite),c(0,10),col="red")
 arrows(limite,0.5,limite+1,0.5,col="red")
}
> ttestsleep(1)
test di compatibilità con 0 (1 coda): pvalue= 0.1087989 
  limite: > -0.2870553  per livello di confidenza= 0.95 

> ttestsleep(2)
test di compatibilità con 0 (1 coda): pvalue= 0.002538066 
  limite: > 1.169334  per livello di confidenza= 0.95

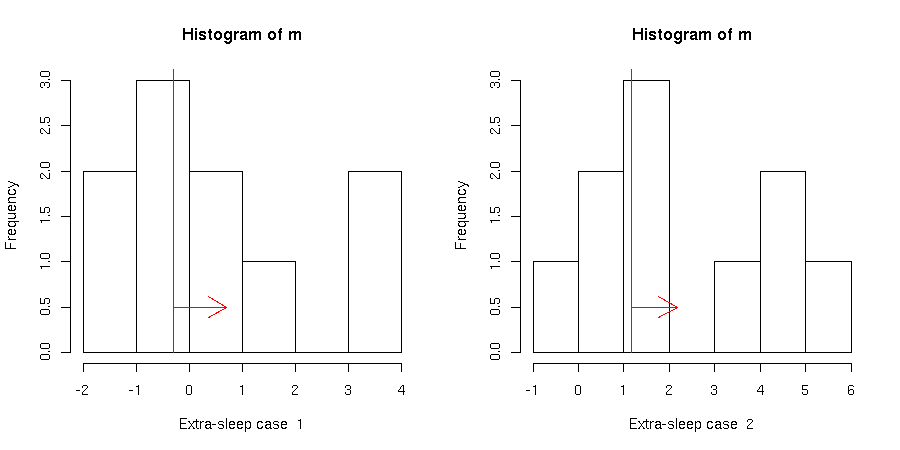
Possiamo dunque concludere che i dati mostrano un effetto significativo solo per il secondo sonnifero.
Il calcolo effettuato è riprodotto dalla funzione di R t.test:

> t.test(subset(sleep,group==1)$extra,alternative="greater")

        One Sample t-test

data:  m 
t = 1.3257, df = 9, p-value = 0.1088
alternative hypothesis: true mean is greater than 0 
95 percent confidence interval:
 -0.2870553        Inf 
sample estimates:
mean of x 
     0.75 

>  t.test(subset(sleep,group==2)$extra,alternative="greater")

        One Sample t-test

data:  subset(sleep, group == 2)$extra 
t = 3.6799, df = 9, p-value = 0.002538
alternative hypothesis: true mean is greater than 0 
95 percent confidence interval:
 1.169334      Inf 
sample estimates:
mean of x 
     2.33

Se più prudentemente volessimo cosiderare anche l'ipotesi alternativa che il sonnifero abbia un effetto negativo sulle ore di sonno, dovremmo fare un test a due code:

ttestsleep2 = function(gr=1,conflevel=0.95) {
 m=subset(sleep,group==gr)$extra
 n=length(m)
 ngl=n-1
 dmean=sd(m)/sqrt(n)
 t=mean(m)/dmean
 cat(" test di compatibilità con 0 (2-code): pvalue=",2*(1-pt(abs(t),df=ngl)),"\n")
 nsigma=qt((1+conflevel)/2,df=ngl)
 cat(" intervallo per livello di confidenza=",conflevel," :", mean(m),
	" +/- ",dmean*nsigma,"\n")
}
> ttestsleep2(1)
 test di compatibilità con 0 (2-code): pvalue= 0.2175978 
 intervallo per livello di confidenza= 0.95  : 0.75  +/-  1.279780

equivalente a

>  t.test(subset(sleep,group==1)$extra,alternative="two.sided")

        One Sample t-test

data:  subset(sleep, group == 1)$extra 
t = 1.3257, df = 9, p-value = 0.2176
alternative hypothesis: true mean is not equal to 0 
95 percent confidence interval:
 -0.5297804  2.0297804 
sample estimates:
mean of x 
     0.75