Soluzione del secondo esercizio

Costruiamo il cerchio di raggio R e centro O' come in figura

Per la simmetria della figura, il cerchio più grande cercato, avrà come centro il punto C a destra di O e sarà tangente agli archi $\stackrel{\frown}{AB}$, $\stackrel{\frown}{BB'}$ e $\stackrel{\frown}{A'B}$, quindi il punto di tangenza P sarà sulla congiungente O'C.
Indichiamo con r=CP il raggio incognito, abbiamo:

O'C=R+r
OA=R-2HM
HM=R-OM

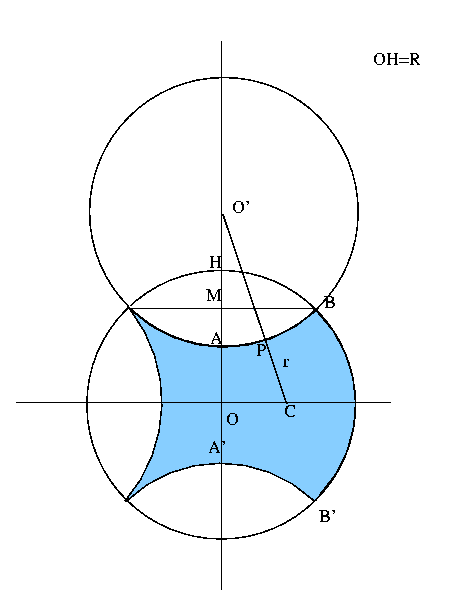
\epsfig{file=gara.eps, height= 8cm}

Avendo OM lunghezza pari alla metà del lato del quadrato inscritto al cerchio, risulta

\begin{displaymath}OM=R\frac{\sqrt{2}}{2} \end{displaymath}

da cui

\begin{displaymath}HM=\frac{2R-r\sqrt{2}}{2},\quad OA=R\sqrt{2}-R, \end{displaymath}

quindi

$OO'=R\sqrt{2}$.

Applicando il teorema di Pitagora al triangolo OCO' si ha:

${OC}^2+{O'O}^2={O'C}^2\Rightarrow (R-r)^2+2R^2=(R+r)^2$,

quindi si ricava

\begin{displaymath}r=\frac{R}{2}.\end{displaymath}

Essendo R=10 il valore cercato è r=5.