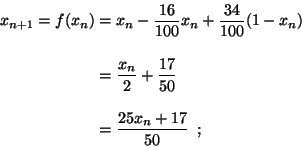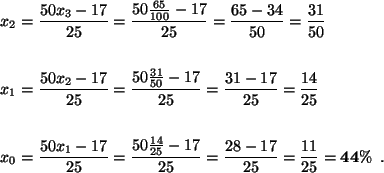Soluzione del terzo esercizio

Indichiamo con xn la percentuale di abitanti nel capoluogo rispetto al totale nell'anno n+2000; pertanto 1-xn rappresenta la percentuale di abitanti in campagna, sempre riferita all'anno n+2000.

Il problema si formula quindi nel modo seguente:

\framebox{\textit{Dato $x_3=\dfrac{65}{100}$ , determinare $x_0$ .}}

La funzione f che esprime xn+1 in funzione di xn è descritta dall'equazione

 \begin{displaymath} \begin{split} x_{n+1}=f(x_n) &=x_n - \frac{16}{100}x_n + \fr... ... \frac{17}{50}\\ \\ &=\frac{25x_n+17}{50}\enspace; \end{split}\end{displaymath} (1)

A questo punto si può procedere in due modi diversi: il primo ha il pregio di essere più naturale, mentre il secondo mette in luce una interessante proprietà di f .

Primo metodo

Conviene scrivere la formula della funzione inversa di f, in modo da esprimere xn in funzione di xn+1 :

\begin{displaymath}x_n=f^{-1}(x_{n+1})=\frac{50x_{n+1}-17}{25}\enspace. \end{displaymath} (2)

Quest'ultima equazione ci permette di procedere a ritroso nel tempo, calcolando dapprima x2, poi x1 e infine il risultato desiderato x0 .


\begin{align*}x_2 &=\frac{50x_3-17}{25} =\frac{50\frac{65}{100}-17}{25} =\frac{6... ...{25}-17}{25} =\frac{28-17}{25}=\frac{11}{25}=\mathbf{44\%}\enspace. \end{align*}

Secondo metodo

Calcoliamo la variazione di x al passare di un anno:


\begin{displaymath}f(x)-x=\frac{x}{2}+\frac{17}{50}-x=\frac{17}{50}-\frac{x}{2}\end{displaymath}

La variazione di x relativa all'anno successivo è

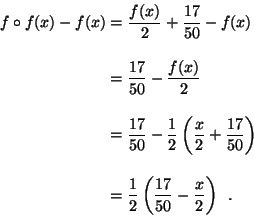
\begin{displaymath}\begin{split} f\circ f(x)-f(x) &=\frac{f(x)}{2}+\frac{17}{50}... ...}{2}\left(\frac{17}{50}-\frac{x}{2}\right)\enspace. \end{split}\end{displaymath}

Da questo calcolo deduciamo che la variazione di x dimezza ogni anno1. Calcoliamo ora la variazione dall'anno 2003 all'anno 2004 (utilizzando per semplicità la notazione percentuale):

\begin{displaymath}f(65\%)-65\%=(32,5\%+34\%)-65\%=66,5\%-65\%=1,5\%\enspace.\end{displaymath}

Per quanto detto sopra, la variazione 2002-2003 è 2 x 1.5% = 3%, la variazione 2001-2002 è 6% e la variazione 2000-2001 è 12%.

La somma di queste tre percentuali (lecita poiché tali percentuali sono tutte riferite al totale degli abitanti, che rimane costante nel tempo) ammonta a 3% + 6% + 12% = 21% ed esprime la variazione di x nel periodo 2000-2003; quindi, nell'anno 2000 gli abitanti del capoluogo sono il 65% - 21% = 44% del totale.

1
Più in generale, se la funzione è del tipo $f(x)=\alpha x + \beta$, la variazione $f\circ f(x)-f(x)$ è pari ad $\alpha[f(x)-x]$