Soluzione del quarto esercizio

Prima parte

I punti, essendo in numero finito, occupano una regione limitata del piano delimitata da un poligono (fig. 1). Possiamo quindi individuare una retta r esterna al poligono. Per fissare le idee supponiamo che la retta in questione sia verticale.

Caso I: non esistono punti equidistanti da r

La retta r lascia tutti i 20 punti in uno stesso semipiano. Traslando la retta r verso destra, potremo individuare via via rette che lasciano alla loro sinistra un punto, due punti, ..., cinque punti individuando così la retta richiesta.

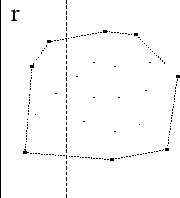
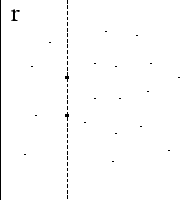$\epsfig{file=fig1.eps,width=4cm}$ $\epsfig{file=fig2.eps,width=4cm}$

fig. 1 fig. 2

Caso II: due o più punti sono equidistanti da r

Rispetto al caso precedente esistono almeno due punti equidistanti da r. Procedendo come sopra, ci sono due o più punti che passano contemporaneamente da una parte all'altra rispetto ad r (fig. 2).

Se i punti equidistanti da r sono il quinto e il sesto (contando a partire dai più vicini ad r) la costruzione precedente fallisce: da 4 punti a sinistra di r passiamo direttamente a 6. Il ragionamento va perfezionato.

Osserviamo innanzitutto che due punti sono equidistanti da r se e solo se r è parallela al segmento che congiunge i due punti (ricordiamo che tutti i punti si trovano nello stesso semipiano rispetto ad r). Per evitare situazioni di equidistanza basterà scegliere r in modo che non sia parallela a nessuno dei segmenti congiungenti una qualunque coppia di punti.

Questo è sempre possibile dato che:

i): Comunque si scelga una direzione, è possibile determinare una retta con tale direzione esterna all'insieme dei punti;
ii): Da un insieme di 20 punti si possono formare $(20\times19)/2=190$ coppie di punti, ovvero abbiamo 190 segmenti distinti che uniscono 2 dei 20 punti. Nella peggiore delle ipotesi, avremo 190 direzioni da scartare per evitare equidistanze;
iii): Le possibili direzioni che una retta può assumere sono infinite.

Abbiamo dimostrato che è sempre possibile trovare una retta r esterna all'insieme dei 20 punti e tale che i 20 punti abbiano 20 distanze distinte dalla retta, riconducendoci così al primo caso.

Seconda parte

Primo metodo

Supponiamo di saper trovare una retta r che separi l'insieme dei 20 punti lasciandone 5 in un semipiano e 15 nell'altro. Fissiamo un punto Q su r e consideriamo le circonferenze tangenti ad r in Q e contenute nel semipiano in cui si trovano i 5 punti. Per ogni punto del semipiano è possibile determinare una tale circonferenza che lo contenga. Scegliendo il raggio abbastanza grande possiamo quindi determinare una circonferenza che contenga i 5 punti e sia contenuta nel semipiano di sinistra. Gli altri 15 punti si trovano nell'altro semipiano e quindi saranno esterni alla circonferenza.

Un procedimento per determinare un possibile centro della circonferenza è il seguente: tracciamo la retta s ortogonale ad r e passante per Q (fig. 3). Congiungiamo Q con P₁ e da quì tracciamo la perpendicolare a QP₁ fino ad intersecare s. Sia T₁ il punto di intersezione. Il triangolo TQP₁ è rettangolo e quindi $\overline{T_1Q}>\overline{T_1P_1}$ . Una circonferenza di centro T₁ e raggio T₁Q conterrà quindi il punto P₁, così come ogni altra circonferenza tangente ad s in Q e con raggio maggiore.

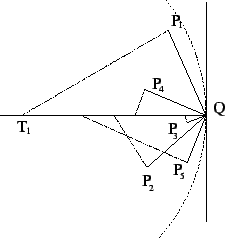$\epsfig{file=fig3.eps,width=5cm}$ fig. 3

Ripetiamo la stessa costruzione per P₂, P₃, P₄ e P₅ individuando su s i punti T₂, T₃, T₄ e T₅. Sia O il punto fra i T_i più lontano da Q. La circonferenza di centro O e raggio OQ contiene esattamente 5 dei 20 punti.

Secondo metodo

La circonferenza richiesta può essere individuata anche indipendentemente dalla costruzione della retta r. Fissiamo un punto Q nel piano e consideriamo le circonferenze di centro Q e raggio via via maggiore. Se non ci sono punti equidistanti da Q i punti entrano nella circonferenza uno alla volta al crescere del raggio. Fermandoci quando 5 punti sono all'interno rispondiamo alla domanda.

Fissati due punti P₁ e P₂, il luogo geometrico dei punti equidistanti da P₁ e P₂ è una retta (asse del segmento P₁P₂). Con 20 punti si possono costruire 190 coppie distinte che individueranno al più 190 rette distinti. Se scegliamo Q in modo che non appartenga a nessuna di queste rette, non esisteranno punti equidistanti da Q permettendo di costruire la circonferenza richiesta.

Terza parte

Sia O il centro della circonferenza $\cal C$ contenente i 20 punti. Il raggio è fissato (sia raggio=R) quindi possiamo soltanto traslare la circonferenza.

Scegliamo una direzione e spostiamo il centro lungo di essa. In generale i punti dell'insieme attraverseranno la circonferenza uno alla volta. Può accadere però che due di essi si trovino ad un certo punto sulla stessa circonferenza, e quindi che passino dall'interno all'esterno contemporaneamente.

Siano P₁ e P₂ due dei 20 punti: esistono soltanto 2 circonferenze passanti per P₁ e P₂ e di raggio R. Quindi fra tutte le circonferenze del piano di raggio R, quelle che ci possono creare problemi sono soltanto 380 ( $2\times 190$ possibili coppie di punti). I segmenti che uniscono O ai centri delle circonferenze appartengono al più a 380 rette distinte.

Scegliendo come direzione in cui trasliamo una diversa da queste 380 siamo certi che i punti usciranno dalla circonferenza uno alla volta. Basterà fermarsi quando la circonferenza conterrà esattamente 5 punti.